Question

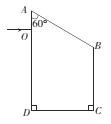
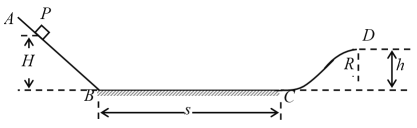
【题目】如图所示，轨道ABCD在竖直平面内，其中AB段为光滑斜面，BC段为粗糙水平面，动摩擦因素为μ，CD是光滑曲面，D为曲面上半径为R的小部分球面的顶点，顶点切线水平，离水平面高为h。质量为m的小物块P在斜面上，若在距水平面高H处由静止释放，物块能沿着轨道ABCD到达D处。不计小物块在B转折处能量的损失。

（1）求物块在水平面上滑行时加速度的大小；

（2）若物块运动到D处时刚好能脱离，求它在C处时的速度；

（3）证明：物块不脱离D点的条件为。

Answer 1

【答案】（1）；（2）；（3）证明见解析

【解析】

（1）物块在水平面上运动时，合力由滑动摩擦力提供，根据牛顿第二定律有

联立解得

（2）当物块到达D点时刚好脱离球面，此时物块的重力提供向心力，有

可得

而物块由C到D，由机械能守恒有

联立解得

（3）证明：物块在斜面上下滑时机械能守恒，有

解得

物块水平面上作匀减速直线运动，有

将和代入，得

即，将代入上式中的，得

当物块到达D点时速度刚好为零，在这种情况下物块在C处时有最小速度，

物块由C到D，机械能守恒，有

可得

将代入中的，得

所以物块不脱离D点的条件为，得证。