题目内容
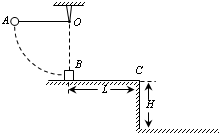 质量mA=0.5kg的小球A系在细线的一端,线的另一端固定在O点,O点到水平面的距离R=0.8m,质量mB=0.3kg的物块B置于高H=1.25m的粗糙的水平桌面上且位于O点正下方,物块B距桌面右边缘的距离L=1m,物块与水平桌面间的动摩擦因数μ=0.45.现拉动小球使线水平伸直,小球由静止开始释放,运动到最低点时与物块发生正碰(碰撞时间极短).碰后,物块B沿桌面滑行并从桌面右边缘飞出,落地点与飞出点的水平距离s=2m.小球与物块均视为质点,不计空气阻力,重力加速度为g=10m/s2,求:
质量mA=0.5kg的小球A系在细线的一端,线的另一端固定在O点,O点到水平面的距离R=0.8m,质量mB=0.3kg的物块B置于高H=1.25m的粗糙的水平桌面上且位于O点正下方,物块B距桌面右边缘的距离L=1m,物块与水平桌面间的动摩擦因数μ=0.45.现拉动小球使线水平伸直,小球由静止开始释放,运动到最低点时与物块发生正碰(碰撞时间极短).碰后,物块B沿桌面滑行并从桌面右边缘飞出,落地点与飞出点的水平距离s=2m.小球与物块均视为质点,不计空气阻力,重力加速度为g=10m/s2,求:(1)小球与物块碰撞后,物块B的速度vB;
(2)小球与物块碰撞后,小球能上升的最大高度h.
分析:(1)物块B离开C后做平抛运动,根据平抛运动的规律求出B以过C点的速度,根据动能定理研究物块B从最低点到C点的过程,即可求出小球与物块碰撞后,物块B的速度vB;
(2)根据机械能守恒求出小球与物块碰撞前的速度大小.对于碰撞过程,根据动量守恒求出碰撞后小球的速度大小,运用机械能守恒求解碰撞后,小球能上升的最大高度h.
(2)根据机械能守恒求出小球与物块碰撞前的速度大小.对于碰撞过程,根据动量守恒求出碰撞后小球的速度大小,运用机械能守恒求解碰撞后,小球能上升的最大高度h.
解答:解:
(1)物块B离开C后做平抛运动,则有:
H=
gt2,s=vCt
则得:vC=s
=2×
m/s=4m/s
物块B从最低点到C点的过程,根据动能定理得:
-μmBgL=
mB
-
mB
得,vB=
=
m/s=5m/s
(2)小球从A到B点的过程,根据动能定理得:
mAgR=
mA
解得,v0=
=
m/s=4m/s
对于碰撞过程,根据动量守恒得:
mAv0=mAvA+mBvB
解得,vA=v0-
vB=4-
×5=1(m/s)
对于小球与物块碰撞后上升过程,由机械能守恒得:
mA
=mAgh
则得,h=
=
m=0.05m
答:
(1)小球与物块碰撞后,物块B的速度vB是5m/s.
(2)小球与物块碰撞后,小球能上升的最大高度h是0.05m.
(1)物块B离开C后做平抛运动,则有:
H=
| 1 |
| 2 |
则得:vC=s
|
|
物块B从最低点到C点的过程,根据动能定理得:
-μmBgL=
| 1 |
| 2 |
| v | 2 C |
| 1 |
| 2 |
| v | 2 B |
得,vB=
|
| 42+2×0.45×10×1 |
(2)小球从A到B点的过程,根据动能定理得:
mAgR=
| 1 |
| 2 |
| v | 2 A |
解得,v0=
| 2gR |
| 2×10×0.8 |
对于碰撞过程,根据动量守恒得:
mAv0=mAvA+mBvB
解得,vA=v0-
| mB |
| mA |
| 0.3 |
| 0.5 |
对于小球与物块碰撞后上升过程,由机械能守恒得:
| 1 |
| 2 |
| v | 2 A |
则得,h=
| ||
| 2g |
| 12 |
| 2×10 |
答:
(1)小球与物块碰撞后,物块B的速度vB是5m/s.
(2)小球与物块碰撞后,小球能上升的最大高度h是0.05m.
点评:本题关键是研究碰撞前A球机械能守恒,碰撞后A球机械能守恒,抓住碰撞过程系统动量也守恒,求出碰撞后小球的速度大小.解决问题首先要清楚研究对象的运动过程.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
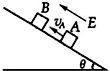 在倾角为θ=37°的足够长的绝缘斜面上,质量mA=0.5kg、带正电的物块A和质量mB=0.25kg的不带电绝缘物块B正沿斜面上滑.斜面处于范围足够大、场强E=5×106N/C、方向平行斜面向上的匀强电场中.当A追上B的瞬间,A的速度v0=1.8m/s,方向沿斜面向上,B的速度恰为零.如图所示,A、B碰撞过程相互作用时间极短,且A的电荷没有转移,碰后瞬间A的速度v1=0.6m/s,方向仍沿斜面向上,碰后经0.60s,A的速率变为v1′=1.8m/s,在这段时间内两者没有再次相碰.已知A和斜面间的动摩擦因数μ=0.15,B与斜面间摩擦可以忽略,A、B均可视为质点,sin37°=0.6,cos37°=0.8,g=10m/s2.求:
在倾角为θ=37°的足够长的绝缘斜面上,质量mA=0.5kg、带正电的物块A和质量mB=0.25kg的不带电绝缘物块B正沿斜面上滑.斜面处于范围足够大、场强E=5×106N/C、方向平行斜面向上的匀强电场中.当A追上B的瞬间,A的速度v0=1.8m/s,方向沿斜面向上,B的速度恰为零.如图所示,A、B碰撞过程相互作用时间极短,且A的电荷没有转移,碰后瞬间A的速度v1=0.6m/s,方向仍沿斜面向上,碰后经0.60s,A的速率变为v1′=1.8m/s,在这段时间内两者没有再次相碰.已知A和斜面间的动摩擦因数μ=0.15,B与斜面间摩擦可以忽略,A、B均可视为质点,sin37°=0.6,cos37°=0.8,g=10m/s2.求: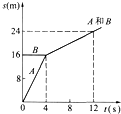 (适合于“侧重理论”的考生)A、B两物体在光滑的水平面上发生碰撞,碰撞前后物体的运动都在同一条直线上.规定A物体原运动方向为正方向.A物体的质量mA=0.5kg.若不计碰撞时间,它们碰撞前后的位移图象如图所示.碰撞前B的质量为mB=
(适合于“侧重理论”的考生)A、B两物体在光滑的水平面上发生碰撞,碰撞前后物体的运动都在同一条直线上.规定A物体原运动方向为正方向.A物体的质量mA=0.5kg.若不计碰撞时间,它们碰撞前后的位移图象如图所示.碰撞前B的质量为mB=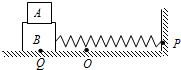 如图,A、B两物体水平叠放在一起,轻弹簧一端与B物体水平相连,另一端固定在墙上P点,物体质量mA=0.5kg、mB=1.5kg,物体B与水平面间的动摩擦因数μ1=0.4,A、B间的动摩擦因数μ2=0.7,弹簧的劲度系数k=200N/m.,现用力F拉物体B,使弹簧从处于自然状态的O点由静止开始向左缓慢移动10cm至Q处,若弹性势能表达式为Ep=
如图,A、B两物体水平叠放在一起,轻弹簧一端与B物体水平相连,另一端固定在墙上P点,物体质量mA=0.5kg、mB=1.5kg,物体B与水平面间的动摩擦因数μ1=0.4,A、B间的动摩擦因数μ2=0.7,弹簧的劲度系数k=200N/m.,现用力F拉物体B,使弹簧从处于自然状态的O点由静止开始向左缓慢移动10cm至Q处,若弹性势能表达式为Ep=