题目内容
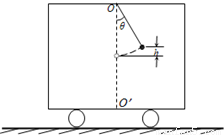
如图所示,在汽车的顶部用不可伸长的细线悬挂一个质量m的小球,以大小为v的初速度在水平面上向右做匀减速直线运动,经过时间t,汽车的位移大小为s(车仍在运动).求:(1)汽车运动的加速度大小;
(2)当小球相对汽车静止时,细线偏移竖直方向的夹角(用反三角函数表示);
(3)汽车速度减小到零时,若小球距悬挂的最低点高度为h,O′点在O点的竖直下方.此后汽车保持静止,当小球摆到最低点时细线恰好被拉断.证明拉断细线后,小球在汽车水平底板上的落点与O'点间的水平距离s与h的平方根成正比.
【答案】分析:(1)根据匀变速直线运动的位移时间公式求出汽车运动的加速度大小.
(2)小球和小车具有相同的加速度,根据小球的加速度,结合牛顿第二定律,平行四边形定则求出细线偏移竖直方向的夹角.
(3)根据机械能守恒定律,结合平抛运动的规律求出水平位移的表达式,得出水平位移和h的关系.
解答:解:(1)由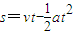 得:
得: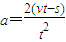 .
.
(2)由受力分析得,小球受到重力与绳子拉力的合力大小为:F=mgtanθ
根据牛顿第二定律,又:F=ma
所以有:
则: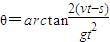 .
.
(3)设小球被细线拉着摆到最低点时的速度为v,
由机械能守恒定律得: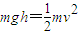
所以: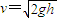
设细线断时小球距离汽车水平底板高度为H,细线断后小球作平抛运动
所以有: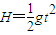
s=vt
解得: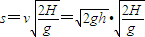 =
=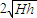 ∝
∝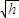 .
.
答:(1)汽车运动的加速度大小为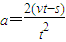 .
.
(2)当小球相对汽车静止时,细线偏移竖直方向的夹角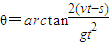 .
.
(3)证明如上所示.
点评:本题综合考查了牛顿第二定律、运动学公式和机械能守恒定律,涉及匀变速直线运动,平抛运动,综合性较强,难度不大,需加强这方面的训练.
(2)小球和小车具有相同的加速度,根据小球的加速度,结合牛顿第二定律,平行四边形定则求出细线偏移竖直方向的夹角.
(3)根据机械能守恒定律,结合平抛运动的规律求出水平位移的表达式,得出水平位移和h的关系.
解答:解:(1)由
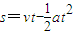 得:
得: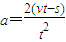 .
.(2)由受力分析得,小球受到重力与绳子拉力的合力大小为:F=mgtanθ
根据牛顿第二定律,又:F=ma
所以有:

则:
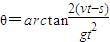 .
.(3)设小球被细线拉着摆到最低点时的速度为v,
由机械能守恒定律得:
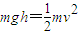
所以:
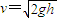
设细线断时小球距离汽车水平底板高度为H,细线断后小球作平抛运动
所以有:
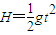
s=vt
解得:
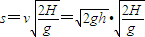 =
=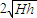 ∝
∝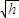 .
.答:(1)汽车运动的加速度大小为
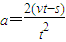 .
.(2)当小球相对汽车静止时,细线偏移竖直方向的夹角
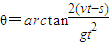 .
.(3)证明如上所示.
点评:本题综合考查了牛顿第二定律、运动学公式和机械能守恒定律,涉及匀变速直线运动,平抛运动,综合性较强,难度不大,需加强这方面的训练.

练习册系列答案
相关题目
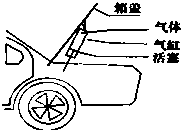 某汽车后备箱内安装有撑起箱盖的装置,它主要由汽缸和活塞组成.开箱时,密闭于汽缸内的压缩气体膨胀,将箱盖顶起,如图所示.在此过程中,若缸内气体与外界无热交换,缸内气体视为理想气体,则缸内气体( )
某汽车后备箱内安装有撑起箱盖的装置,它主要由汽缸和活塞组成.开箱时,密闭于汽缸内的压缩气体膨胀,将箱盖顶起,如图所示.在此过程中,若缸内气体与外界无热交换,缸内气体视为理想气体,则缸内气体( )| A、对外做负功,分子的平均动能增大 | B、对外做负功,分子的平均动能减小 | C、对外做正功,内能减小 | D、对外做正功,内能增大 |
 如图所示,当汽车通过拱桥顶点的速度为10m/s时,车对桥顶的压力为车重的3/4,如果要使汽车在粗糙的桥面行驶至桥顶时,不受摩擦力作用,则汽车通过桥顶的速度应为(g=10m/s2)( )
如图所示,当汽车通过拱桥顶点的速度为10m/s时,车对桥顶的压力为车重的3/4,如果要使汽车在粗糙的桥面行驶至桥顶时,不受摩擦力作用,则汽车通过桥顶的速度应为(g=10m/s2)( ) 如图所示,当汽车通过拱桥顶点的速度为5m/s时,车对桥顶的压力为车重的
如图所示,当汽车通过拱桥顶点的速度为5m/s时,车对桥顶的压力为车重的 如图所示,一汽车通过拱形桥顶点时的速率是v、汽车对拱形桥压力是车重的
如图所示,一汽车通过拱形桥顶点时的速率是v、汽车对拱形桥压力是车重的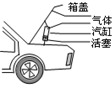 某汽车后备箱内安装有撑起箱盖的装置,它主要由汽缸和活塞组成.开箱时,密闭于汽缸内的压缩气体膨胀,将箱盖顶起,如图所示.在此过程中,若缸内气体与外界无热交换,忽略气体分子间相互作用,则缸内气体( )
某汽车后备箱内安装有撑起箱盖的装置,它主要由汽缸和活塞组成.开箱时,密闭于汽缸内的压缩气体膨胀,将箱盖顶起,如图所示.在此过程中,若缸内气体与外界无热交换,忽略气体分子间相互作用,则缸内气体( )