��Ŀ����
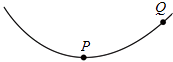
����Ŀ����ˮƽ������һ������ΪL=2m������ΪM=1kg��ľ��P����ľ�������������һ������Ϊm=2kg��С����Q��PQ֮�䶯Ħ������Ϊ��1=0.2��P��ˮƽ��֮�䶯Ħ������Ϊ��2=0.4��ϵͳ��ֹ��![]()
��1������Qʩ��һ��ˮƽ���ҵĺ���F=16N����ʹQ��P�ϵ���ȥ����F��Q����Ҫ�����ٹ���
��2������Pʩ��һ��ˮƽ���ҵĺ���F=15N����ʹQ��P�ϵ���ȥ����F�������ʱ�䣿
���𰸡�
��1��
�⣺PQһ����ٵ������ٶ�Ϊ ![]()
PQ��Ħ����f1=��1mg=0.2��2��10N=4N
P��ˮƽ���Ħ����Ϊf2=��2��M+m��g=0.4����1+2����10N=12N
��f1��f2
��P��ֹ
Q���ٶ�Ϊ����ţ�ٵڶ����ɵ�
F����1mg=ma1
![]()
��ȥF��P�ļ��ٶ�Ϊ ![]()
��ȥF��ǡ�û���P���Ҷ��ٶȼ�Ϊ�㣬��ʱF�������٣���x= ![]() ֪����ȥFǰ��λ��֮��Ϊ1��3��
֪����ȥFǰ��λ��֮��Ϊ1��3��
![]()
WF=Fx1=16��0.25J=4J
��2��
�⣺��ʩ��F��һ����٣��� ![]()
��P��Qһ����������ʱ��t2
��v=a1t2
��ȥF�� ![]()
![]()
��P��ֹͣ��QֹͣP�����Ҷ�ʱ��F����ʱ�����
![]()
![]()
t1=2.3s
����������1��ͨ������PQһ�����ʱ�ļ��ٶȺ����ܵ���Ħ�������жϳ�PQ���˶��������ţ�ٵڶ�����������ٶȣ���Q�պ��˶���P��ʱ���ٶȼ����㣬�����������٣����ɵ�ѧ��ʽ���λ�ƹ�ϵ���������������������2��������������P��ʱ����ţ�ٵڶ����������ͬ�ļ��ٶȣ������˶�ѧ��ʽ���ʱ�䣮