题目内容
【题目】如图所示,半径为0.1m的竖直圆环上固定有一个质量为0.1 kg的小球,圆环绕其圆心在竖直面内以角速度![]() =7rad/s沿逆时针方向匀速转动。已知重力加速度g取9.8 m/s2,小球由P点转动到Q点的过程中,下列说法正确的是
=7rad/s沿逆时针方向匀速转动。已知重力加速度g取9.8 m/s2,小球由P点转动到Q点的过程中,下列说法正确的是
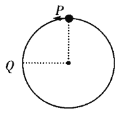
A.小球重力的功率先增大后减小
B.圆环对小球的作用力先减小后增大
C.圆环对小球的作用力与竖直方向的最大夹角为30°
D.圆环对小球的作用力的最小值为0.98 N
【答案】C
【解析】
A.小球随圆环匀速转动,由P点转到Q点的过程中,竖直分速度越来越大,因此重力的功率越来越大,故A错误;
BD.圆环由P到Q转动过程中,由牛顿第二定律:![]() (其中α为圆环所在位置与圆心连线与竖直方向的夹角),当α=0时FN=-0.49N,方向竖直向上;当α=90°时FN=0.49N,则随着α增大,FN先减小到0后变大,圆环对小球的作用力的最小值为0,故BD错误;
(其中α为圆环所在位置与圆心连线与竖直方向的夹角),当α=0时FN=-0.49N,方向竖直向上;当α=90°时FN=0.49N,则随着α增大,FN先减小到0后变大,圆环对小球的作用力的最小值为0,故BD错误;
C.小球受到的向心力F向=mω2r=0.49N,如图所示,以小球所处的位置为圆心,以0.49N为半径作圆,可知圆环对小球的作用力F与圆相切时,夹角θ最大,![]() ,则θ=30°,故C正确;
,则θ=30°,故C正确;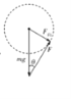

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目