题目内容
（12分）如图所示．一固定足够长的斜面MN与水平面的夹角α＝37°，斜面上有一质量为m=1kg的小球P，Q是一带竖直推板的直杆。现使竖直杆Q以水平加速度a＝4m/s2水平向右从斜面底N开始做初速为零的匀加速直线运动，从而推动小球P沿斜面向上运动．小球P与直杆Q及斜面之间的摩擦均不计，直杆Q始终保持竖直状态，求：（sin37°＝0.6）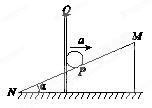
⑴该过程中小球P的加速度大小，直杆Q对小球P的推力大小．
⑵直杆Q从开始推动小球P经时间t=0.6s后突然停止运动并立即撤出，小球P由于惯性向上滑动达最高点到N点的距离及返回到N点所用时间？(可以用根式表示)
（1）5m/s2 ，18.33N（2）1.65m,1.2s
解析试题分析(1) 对小球P进行受力分析，受力图如图所示，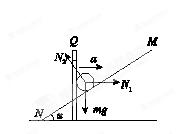
根据牛顿第二定律可得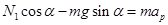
又有：
联立以上各式解得aP＝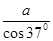
＝5m/s2，(3分)
N1＝55/3N=18.33N（3分）
（2）小球在0.6s内做匀加速直线运动，位移为：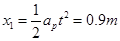
0.6s后的速度为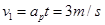
撤去直杆Q后，小球P做匀减速运动，其加速度为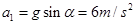
减速到零的位移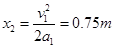
小球达到最高点时与N点的距离：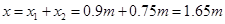
对小球匀减速运动直到回到N点的过程有: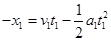
解得时间为：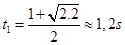
考点：本题考查了牛顿第二定律和匀变速直线运动规律
练习册系列答案
相关题目
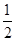，求：
