题目内容
如图所示，质量为m2和m3的物体静止在光滑的水平面上，两者之间有压缩着的弹簧，一个质量为m1的物体以速度v向右冲来，为了防止冲撞，m2物体将m3物体以一定速度弹射出去，设m1与m3碰撞后粘合在一起，则m3的弹射速度至少为多大，才能使以后m3和m2不发生碰撞？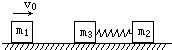
【答案】分析：m2物体将m3物体的过程和m1与m3碰撞的过程，系统的动量均守恒，当m1与m3碰撞后两者的共同速度与m2的速度相等时，m3和m2恰好不发生碰撞，对两个过程由动量守恒定律列式，并结合条件可以求出m3的弹射速度．
解答：解：以向右为正方向，m2物体将m3物体弹开时动量守恒，有：0=m2v2-m3v3 ①
m1与m3碰撞动量守恒，有 m1v1-m3v3=（m1+m3）v ②，
若m3和m2恰好不发生碰撞，则有 v=v3 ③
联立以上三式得 v3=
答：m3的弹射速度至少为
，才能使以后m3和m2不发生碰撞．
点评：应用动量守恒定律即可正确解题，应用动量守恒定律解题时，要注意过程的分析与研究对象的选择．
解答：解：以向右为正方向，m2物体将m3物体弹开时动量守恒，有：0=m2v2-m3v3 ①
m1与m3碰撞动量守恒，有 m1v1-m3v3=（m1+m3）v ②，
若m3和m2恰好不发生碰撞，则有 v=v3 ③
联立以上三式得 v3=
答：m3的弹射速度至少为
，才能使以后m3和m2不发生碰撞．点评：应用动量守恒定律即可正确解题，应用动量守恒定律解题时，要注意过程的分析与研究对象的选择．
练习册系列答案
相关题目
（2011?娄底模拟）如图所示，质量为m2的物体2放在正沿平直的轨道向右行驶的车厢底板上，并用竖直细绳通过定滑轮连接质量为m1的物体1，与物体1相连接的绳与竖直方向成β角，则（ ）
（1）天然放射性元素23290Th（钍）经过一系列α衰变和β衰变之后，变成20882Pb（铅）．下列论断中止确的是
如图所示，质量为m2的小球B静止在光滑的水平面上，质量为m1的小球A以速度v0靠近B，并与B发生碰撞，碰撞前后两个小球的速度始终在同一条直线上．A、B两球的半径相等，且碰撞过程没有机械能损失．当m1、v0一定时，若m2越大，则（ ）| A、碰撞后A的速度越小 | B、碰撞后A的速度越大 | C、碰撞过程中B受到的冲量越小 | D、碰撞过程中A受到的冲量越大 |
（1）下列说法中正确的是
如图所示，质量为m2的物体2放在车厢的水平底板上，用竖直细绳通过光滑定滑轮与质量为m1的物体1相连．车厢正沿水平直轨道向右行驶，此时与物体1相连的细绳与竖直方向成θ角，由此可知（ ）| A、车厢的加速度大小为gsinθ?? | ||
B、绳对m1的拉力大小为
| ||
| C、底板对物体2的支持力大小为（m2-m1）g?? | ||
| D、底板对m2的摩擦力大小为m2gtanθ |