题目内容
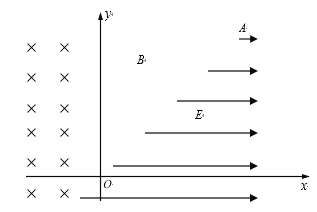
【题目】如图所示,在直角坐标系xoy 中,OA与x轴的夹角为45°,在OA的右侧有一沿 x轴正方向的匀强电场,电场强度为E,在OA的左侧区域及第二象限区域有垂直纸面向里的匀强磁场,磁感应强度为B,在x轴上的某点静止释放一个质量为m、带电量为q且不计重力的带电粒子(不计重力),粒子将向左运动进入磁场,问:
(1)若释放点的位置坐标为x0,则粒子进入磁场后经过 y 轴时的坐标为多少?
(2)若上述粒子在返回电场后,经过x轴前没有进入磁场,则粒子从释放到又经过 x 轴需多长时间?
(3)若粒子在x轴上的 P点释放后,粒子在进出磁场一次后又返回到P点,求P点的位置坐标是多少?
【答案】(1) ![]() (2)
(2) ![]() (3)
(3) ![]()
【解析】
(1)带电粒子在电场中加速![]() ,在磁场中受洛伦兹力向上,粒子沿顺时针方向偏转
,在磁场中受洛伦兹力向上,粒子沿顺时针方向偏转
![]()
粒子从O点进入磁场,经过半个周期经过y轴,故其坐标为
![]()
(2)粒子回到OA边界时,转过了四分之三圆弧,又进入电场,此时速度方向垂直于电场,粒子在电场中做类平抛运动,沿垂直于电场方向位移为R时经过x轴,故
从静止开始加速运动到磁场,
![]()
![]()
磁场中运动,![]()
电场中运动的类平抛运动时间![]()
得
![]()
(3)由第(2)小题的分析可知,若![]() ,则粒子恰回到出发点,即
,则粒子恰回到出发点,即
![]()
解得
![]()

练习册系列答案
相关题目