题目内容
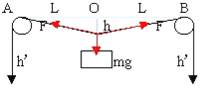
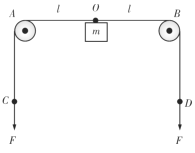
【题目】如图所示,轻质长绳水平地跨在相距2![]() 的两个小定滑轮A、B上,质量为m的物块悬挂在绳上O点,O与A、B两滑轮的距离相等.在轻绳两端C、D分别施加竖直向下的恒力F=mg.先托住物块,使绳处于水平拉直状态,静止释放物块,在物块下落过程中,保持CM两端的拉力F 不变.
的两个小定滑轮A、B上,质量为m的物块悬挂在绳上O点,O与A、B两滑轮的距离相等.在轻绳两端C、D分别施加竖直向下的恒力F=mg.先托住物块,使绳处于水平拉直状态,静止释放物块,在物块下落过程中,保持CM两端的拉力F 不变.
(1)当物块下落距离h为多大时,物块的加速度为零?
(2)在物块下落上述距离的过程中,克服C端恒力F做功W为多少?
(3)求物块下落过程中的最大速度Vm和最大距离H.
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]() ,
,![]()
【解析】
试题由静止释放后,由于绳OC和绳OB对物块的合力小于重力,所以物块向下先作加速运动,随着物块的下落,两绳间的夹角逐渐减小.因为绳子对物块的拉力大小不变,恒等于F,所以随着两绳间的夹角减小,两绳对物块拉力的合力将逐渐增大,物块所受的合力逐渐减小,向下加速度逐渐减小.当物两绳的合力等于物块的重力时,即块的合外力为零时,速度达到最大值vm.故加速度为零时重力等于两绳的合力.之后,因为两绳间夹角继续减小,两绳合力大于物块的重力,物块所受合外力竖直向上,且逐渐增大,物块将作加速度逐渐增大的减速运动.当物块下降速度减为零时,物块竖直下落的距离达到最大值H.当物块的加速度为零时,由共点力平衡条件可求出相应的θ角,再由θ角求出相应的距离h,进而求出克服C端恒力F所做的功.对物块运用动能定理可求出物块下落过程中的最大速度Vm和最大距离H.
(1)故加速度为零时应有重力等于两绳的合力.
(2)由加速度为零时下落的高度h,可以由几何关系解出C点向上运动的距离,从而可以求出F做的功WF,故克服力F做的功为﹣WF
(3)由于下落h时速度为vm,故由动能定理即可求出vm;物块速度为零时下落距离为H,由动能定理求解H.
解:(1)当物块所受的合外力为零时,加速度为零,此时物块下降距离为h.因为F恒定,所以两绳对物块拉力大小分别为F,两绳与竖直方向夹角均为θ,由平衡条件知:
2Fcosθ=mg2θ=120°,所以θ=60°,
由图知:h=Ltan30°=![]() L ①
L ①
(2)物块下落h时,绳的C、D端均上升h′由几何关系可得:h′=![]() ﹣L ②
﹣L ②
克服C端恒力F做的功为:W=Fh′③
由①②③式联立解得:W=(![]() ﹣1)mgL
﹣1)mgL
(3)在物块下落过程中,共有三个力对物块做功.重力做正功,两端绳子对物块的拉力做负功.两端绳子拉力做的功就等于作用在C、D端的恒力F所做的功.因为物块下降距离h时动能最大.由动能定理得:mgh﹣2W=![]() ④
④
将①②③式代入④式解得:vm=![]()
当物块速度减小为零时,物块下落距离达到最大值H,绳C、D上升的距离为H’.由动能定理得:
mgH﹣2mgH′=0,又H′=![]() ﹣L,
﹣L,
联立解得:H=![]() .
.
答:(1)当物块下落距离h为![]() 时,物块的加速度为零.
时,物块的加速度为零.
(2)在物块下落上述距离的过程中,克服C端恒力F做功W为(![]() ﹣1)mgL.
﹣1)mgL.
(3)物块下落过程中的最大速度vm为![]() ,最大距离H为
,最大距离H为![]() .
.