题目内容
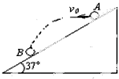在倾角为37°的斜面上，从A点以6m/s的初速度水平抛出一个小球，小球落在B点，如图所示．则A、B两点间的距离分析：平抛运动在水平方向上做匀速直线运动，在竖直方向上做自由落体运动，根据竖直位移与水平位移的关系求出运动的时间，从而得出水平距离和竖直分速度，结合平行四边形定则求出AB的距离．
解答：解：小球做平抛运动，运动轨迹如图，设小球运动的时间为t，
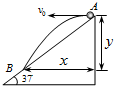
在你水平方向：x=v0t，
竖直方向：y=
gt2，
结合几何知识：tan37°=
，
解得：t=
=0.9s，
水平位移：x=v0t=6×0.9m=5.4m．
AB间的距离s=
=6.75m．
故答案为：6.75；0.9．
在你水平方向：x=v0t，
竖直方向：y=
| 1 |
| 2 |
结合几何知识：tan37°=
| y |
| x |
解得：t=
| 3v0 |
| 2g |
水平位移：x=v0t=6×0.9m=5.4m．
AB间的距离s=
| x |
| cos37° |
故答案为：6.75；0.9．
点评：解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律，结合运动学公式灵活求解．
练习册系列答案
相关题目
质量为4kg的物块在倾角为37°的斜面顶端由静止开始下滑，已知物块与斜面间的动摩擦因数μ=0.1，斜面长为5.2m．
如图所示，在倾角为θ=37°的斜面两端，垂直于斜面方向固定两个弹性板，两板相距d=2m，质量为m=10g，带电量为q=+1×10-7C的物体与斜面间的动摩擦因数为μ=0.2，物体从斜面中点以大小为v0=10m/s的速度沿斜面开始运动．若物体与弹性板碰撞过程中机械能不损失，电量也不变，匀强电场（方向与斜面平行）的场强E=2×106N/C，求物体在斜面上运动的总路程．（g取10m/s2 sin37°=0.6 cos37°=0.8）
一重量G为10N的木块静止在倾角为37°的斜面上则它所受到的静摩擦力为（sin37°=0.6cos37°=0.8）（ ）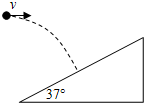
如图所示，在倾角为37°的斜面底端正上方某处，以速度v0﹦6m/s水平抛出一小球，忽略空气阻力，该小球恰好垂直打在斜面上的一点，求小球抛出时距离斜面底端的高度．（sin37°﹦0.6，cos37°﹦0.8，g=l0m/s2）