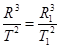题目内容
我国发射的“嫦娥一号”探月卫星沿近似于圆形的轨道绕月飞行.为了获得月球表面全貌的信息,让卫星轨道平面缓慢变化.卫星将获得的信息持续用微波信号发回地球.设地球和月球的质量分别为M和m,地球和月球的半径分别为R和R1,月球绕地球的轨道半径和卫星绕月球的轨道半径分别为r和r1,月球绕地球转动的周期为T.假定在卫星绕月运行一个周期内卫星轨道平面与地月连心线共面.求在该周期内卫星发射的微波信号因月球遮挡而不能到达地球的时间(有M?m?R?R1?r?r1和T表示,忽略月球绕地球转动对遮挡时间的影响).
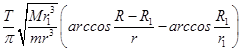
如图,O和O′分别表示地球和月球的中心.在卫星轨道平面上,A是地月连心线OO′与地月球面的公切线ACD的交点,D?C和B分别是该公切线与地球表面?月球表面和卫星圆轨道的交点.根据对称性,过A点的另一侧作地月球面的公切线,交卫星轨道于E点.卫星在上运动时发出的信号被遮挡.
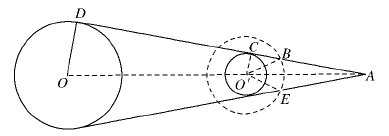
设探月卫星的质量为m0,万有引力常量为G,根据万有引力定律有
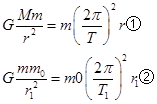
式中,T1是探月卫星绕月球转动的周期.由①②式得
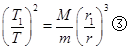
设卫星的微波信号被遮挡的时间为t,则由于卫星绕月做匀速圆周运动,应用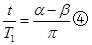
式中,α=∠CO′A,β=∠CO′B.由几何关系得
rcosα=R-R1⑤
r1cosβ=R1⑥
由③④⑤⑥式得
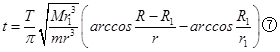

设探月卫星的质量为m0,万有引力常量为G,根据万有引力定律有
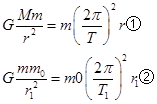
式中,T1是探月卫星绕月球转动的周期.由①②式得
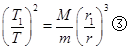
设卫星的微波信号被遮挡的时间为t,则由于卫星绕月做匀速圆周运动,应用
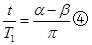
式中,α=∠CO′A,β=∠CO′B.由几何关系得
rcosα=R-R1⑤
r1cosβ=R1⑥
由③④⑤⑥式得
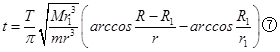

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目

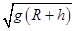


 ,则轨道半径之比和运动速率之比分别为( )
,则轨道半径之比和运动速率之比分别为( ) B.
B. 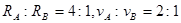
 D.
D. 
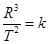 ,下列说法正确的是
,下列说法正确的是