Question

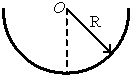
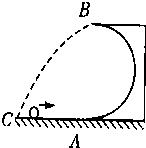
质量为m的小球在半径为R的光滑竖直圆环内做圆周运动，重力加速度大小为g，不计空气阻力．下列说法正确的是（　　）

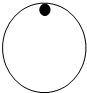
A．小球经过最低点的最小速度为 gR

B．小球经过最低点的最小速度为 5gR

C．圆环最低点和最高点对小球的压力大小的差值为2mg

D．圆环最低点和最高点对小球的压力大小的差值为6mg

Answer 1

A、B、在最高点，弹力和重力的合力提供向心力，根据牛顿第二定律，有：
F₁+mg=m

v 21

R

当F₁=0时，v₁有最小值

gR

；
对从最高点到最低点过程，根据动能定理，有：
mg?2R=

1

2

m

v

22

-

1

2

m

v

21

将v₁的最小值

gR

代入，得到v₂的最小值为

5gR

；
故A错误，B正确；
C、D、在最高点，弹力和重力的合力提供向心力，根据牛顿第二定律，有：
F₁+mg=m

v 21

R

①
在最低点，弹力和重力的合力提供向心力，根据牛顿第二定律，有：
F₂-mg=m

v 22

R

②
压力差：
△F=F₂-F₁ ③
对从最高点到最低点过程，根据动能定理，有：
mg?2R=

1

2

m

v

22

-

1

2

m

v

21

④
联立①②③④解得：
△F=6mg
故C错误，D正确；
故选：BD．