Question

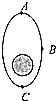
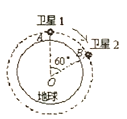
【题目】“北斗”系统中两颗工作卫星1和2在同一轨道上绕地心O沿顺时针方向做匀速圆周运动，轨道半径为r，某时刻它们分别位于轨道上的A，B两位置，如图所示，已知地球表面处的重力加速度为g，地球半径为R，不计卫星间的相互作用力，以下判断正确的是（）

A. 这两颗卫星的向心加速度大小为

B. 这两颗卫星的角速度大小为

C. 卫星1由位置A运动至位置B所需时间为

D. 如果使卫星1 加速，它就一定能追上卫星2

Answer 1

【答案】C

【解析】

根据万有引力提供向心力得出加速度与轨道半径的关系；根据万有引力提供向心力，求出角速度的大小，从而求出卫星1由位置A运动到位置B所需的时间；卫星1在轨道上若加速，所受的万有引力不够提供向心力，做离心运动离开原轨道，不会追上卫星2。

A、卫星绕地球做匀速圆周运动，万有引力充当向心力，即：，由万有引力与重力关系，，解两式得：，故A错误；

B、由，将上式代入得：，故B错误；

C、卫星1由位置A运动到位置B所需时间为卫星周期的，由，得，故C正确；

D、卫星1加速后做离心运动，进入高轨道运动，不能追上卫星2，故D错误；

故选C。