题目内容
如图所示，位于竖直平面内的固定光滑圆环与水平面相切于M点，环心在O处，环上N点与之等高，NM为一光滑直轨，质点小球a自N处从静止开始沿NM运动到M点，而小球b则由O点起自由落体到M点，关于两球运动时间的长短关系为( )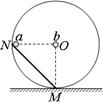
| A．a长 | B．b长 |
| C．一样长 | D．不好比较 |
A
解析试题分析：设固定光滑圆环的半径为R，根据图中几何关系可知，NM直轨的倾角为45°，由牛顿第二定律可知，小球运动的加速度为gsin45°，位移为R/sin45°，根据匀变速直线运动位移公式解得小球a运动的时间为：ta＝
＝
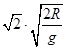，根据自由落体运动规律解得小球b运动的时间为：tb＝
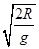，所以有：ta＞tb，故选项A正确。
考点：本题主要考查了匀变速直线运动规律和牛顿运动定律的应用问题，属于中档偏低题。
在平直公路上，汽车以15m/s的速度做匀速直线运动，从某时刻开始刹车，在阻力作用下，汽车以2m/s2的加速度做匀减速直线运动，则刹车后10s内汽车的位移大小为（ ）
| A．50m | B．56.25m |
| C．75m | D．150m |
一质点做初速度为零的匀加速直线运动，经时间T 通过位移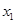
到达A点，接着在时间T 内又通过位移
到达B点，则以下推断正确的有
A．物体通过A点时的速度为 |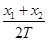
B．物体运动的加速度为 |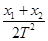
| C．物体通过B点时的速度为 |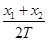
D．物体运动的加速度为 |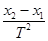
一个做匀加速直线运动的物体，先后经过a、b两点时的速度分别是v和7v，通过ab段的时间是t，则下列判断正确的是
| A．经过ab中点的速度是4v |
| B．经过ab中间时刻的速度是4v |
| C．前t/2时间通过的位移比后t/2时间通过的位移少l.5vt |
| D．前1/2位移所需的时间是后1/2位移所需时间的2倍 |
一条足够长的浅色水平传送带自左向右匀速运行，现将一个木炭包无初速地放在传送带的最左端，木炭包在传送带上将会留下一段黑色的径迹。下列说法中正确的是（ ）
| A．黑色的径迹将出现在木炭包的左侧 |
| B．木炭包的质量越大，径迹的长度越短 |
| C．传送带运动的速度越大，径迹的长度越短 |
| D．木炭包与传送带间动摩擦因数越大，径迹的长度越短 |
可看成质点的物体做匀加速直线运动，先后经过a、b两点时的速度分别为v和7v，由a到b所用时间为t，则下列判断正确的是（ ）
A．质点运动的加速度大小为 |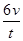
| B．质点经过ab中点的速度为5v |
C．质点在ab间前一半时间通过的位移是后一半时间通过的位移的 |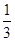
| D．质点在ab间前一半位移所用时间是后一半位移所用时间的2倍 |
下列说法正确的是（ ）
| A．若物体运动速率始终不变，则物体所受合力为零 |
| B．若物体的加速度均匀增加，则物体做匀加速直线运动 |
| C．若物体的加速度与其速度方向相反，则物体做匀减速直线运动 |
| D．若物体在任意的相等时间间隔内位移相等，则物体做匀速直线运动 |
如图所示，劲度数为k的轻弹簧的一端固定在墙上，另一端与置于水平面上质量为m的物体接触(未连接)，弹簧水平且无形变，用水平力F缓慢推动物体，在弹性限度内弹簧长度被压缩了x0，此时物体静止，撤去F后，物体开始向左运动，运动的最大距离为4x0，物体与水平面间的动摩擦因数为μ，重力加速度取g，则( )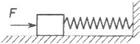
| A．撤去F后，物体先做匀加速运动，再做匀减速运动 |
B．撤去F后，物体刚运动时的加速度大小为 －μg |
C．物体做匀减速运动的时间为 |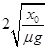
D．物体开始向左运动到速度最大的过程中克服摩擦力做的功为μmg(x0－ ) |