题目内容
质量为m=1.0kg的小滑块(可视为质点)放在质量为M=3.0kg的长木板的右端,木板上表面光滑,木板与地面之间的动摩擦因数为μ=0.2,木板长为L.开始时两者都处于静止状态,现对木板施加水平向右的恒力F=l2N,如图所示.为使小滑块不掉下木板,水平恒力F允许作用的最长时间为1s.(g取l0m/s2)求:
(1)在0~1s时间内长木板在的加速度大小;
(2)木板的长度L.
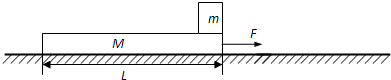
(1)在0~1s时间内长木板在的加速度大小;
(2)木板的长度L.

分析:(1)根据牛顿第二定律求出拉力F作用时M的加速度大小.
(2)根据牛顿第二定律求出撤去拉力F后的加速度大小,木板先做匀加速直线运动,再做匀减速直线运动,抓住两段位移之和等于木板的长度,运用运动学公式求出木板的长度.
(2)根据牛顿第二定律求出撤去拉力F后的加速度大小,木板先做匀加速直线运动,再做匀减速直线运动,抓住两段位移之和等于木板的长度,运用运动学公式求出木板的长度.
解答:解:(1)撤力前后木板先加速后减速,设加速过程的位移为x1,加速度为a1,加速运动的时间为t1;减速过程的位移为x2,加速度为a2,减速运动的时间为t2.由牛顿第二定律有
撤力前:F-μ(m+M)g=Ma1…①
解得a1=
m/s2…②
(2)撤力后:μ(M+m)g=Ma2…③
解得a2=
m/s2
x1=
a1t12,x2=
a2t22…④
木块恰好不从木板上掉下,应满足x1+x2=L…⑤
又a1t1=a2t2…⑥
由以上各式可解得L=1m…⑦
答:(1)在0~1s时间内长木板在的加速度大小为
m/s2.
(2)木板的长度L为1m.
撤力前:F-μ(m+M)g=Ma1…①
解得a1=
| 4 |
| 3 |
(2)撤力后:μ(M+m)g=Ma2…③
解得a2=
| 8 |
| 3 |
x1=
| 1 |
| 2 |
| 1 |
| 2 |
木块恰好不从木板上掉下,应满足x1+x2=L…⑤
又a1t1=a2t2…⑥
由以上各式可解得L=1m…⑦
答:(1)在0~1s时间内长木板在的加速度大小为
| 4 |
| 3 |
(2)木板的长度L为1m.
点评:解决本题的关键能够正确地受力分析,运用牛顿第二定律和运动学公式联合求解.

练习册系列答案
相关题目
 如图所示,质量为m=1.0kg的小球从H=20m高处水平抛出的小球,除受重力外,还受到水平风力作用,假设受到的风力的大小恒定不变,g=10m/s2.问:
如图所示,质量为m=1.0kg的小球从H=20m高处水平抛出的小球,除受重力外,还受到水平风力作用,假设受到的风力的大小恒定不变,g=10m/s2.问:

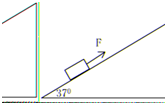 如图示,在倾角为37°的足够长的斜面底端有一质量为m=1.0kg的物体,现用绳将物体由静止沿斜面向上拉动,拉力F=10N,方向平行与斜面向上,物体以2m/s2向上匀加速运动.经时间t1=4秒时绳子断了.(sin37°=0.6 cos37°=0.8 g=10m/s2)求:
如图示,在倾角为37°的足够长的斜面底端有一质量为m=1.0kg的物体,现用绳将物体由静止沿斜面向上拉动,拉力F=10N,方向平行与斜面向上,物体以2m/s2向上匀加速运动.经时间t1=4秒时绳子断了.(sin37°=0.6 cos37°=0.8 g=10m/s2)求: