题目内容
7.小船要在平直河道中渡到对岸,河宽为300m,水流速度是6m/s(假设河两边的流速与河中央的流速一样大),小船在静水中的航速是10m/s.(cos53°=0.6,cos37°=0.8)求:(1)要使小船渡河时间最少,渡河最短时间为多少?
(2)要使小船渡河航程最短,小船船头方向与河岸上游的夹角为多少度?
(3)如果另一小船要在该河道渡河,该船在静水中的航速是4.8m/s,要使渡河航程最短,该小船船头方向与河岸上游的夹角为多少度?渡河最短航程为多少?
分析 (1)、船头始终垂直与河岸时,渡河时间最短,由运动学公式即可得知渡河的最短时间.
(2)、当船的合速度方向垂直于河岸时,船能垂直渡河,对船在静水中的速度进行正交分解,即可得知小船船头方向与河岸上游的夹角.
(3)、当船在静水中的速度要与合速度垂直时,合速度与河岸的夹角最大,此时渡河位移最短,由几何关系可得知小船船头方向与河岸上游的夹角及渡河最短航程.
解答  解:(1)、当船头始终垂直于河岸航行时,渡河时间最短.有:
解:(1)、当船头始终垂直于河岸航行时,渡河时间最短.有:
t=$\frac{d}{{v}_{静}}$=$\frac{300}{10}$=30s
(2)、要使小船渡河航程最短,就是使得船的合速度垂直于河岸,此时,船在静水中的速度沿河岸的分量与水流的速度大小相等,方向相反,设小船船头方向与河岸上游的夹角为θ,如图1所示,有:
v静cosθ=v水
得:cosθ=$\frac{{v}_{水}}{{v}_{静}}$=$\frac{6}{10}$=0.6 得:θ=53°
得:θ=53°
(3)、另一小船要在该河道渡河,该船在静水中的航速是4.8m/s,要使渡河航程最短,船在静水中的速度要与合速度垂直,设此时小船船头方向与河岸上游的夹角为α,如图2所示,则有:
cosα=$\frac{{v}_{静}^{′}}{{v}_{水}}$=$\frac{4.8}{6}$=0.8
得:α=37°
由几何关系可得最短航程为:s=$\frac{{v}_{水}}{{v}_{静}^{′}}$d=$\frac{6}{4.8}$×300=375m
答:(1)要使小船渡河时间最少,渡河最短时间为30s.
(2)要使小船渡河航程最短,小船船头方向与河岸上游的夹角为53°.
(3)如果另一小船要在该河道渡河,该船在静水中的航速是4.8m/s,要使渡河航程最短,该小船船头方向与河岸上游的夹角为37°,渡河最短航程为375m
点评 该题通过渡河的模型考察了运动的合成与分解,关于渡河问题,应注意几种渡河方式:
一是垂直渡河,此时渡河位移最短,但是所用时间不是最短的,此种情况要求船的合速度与河岸垂直,
二是船头始终指向对岸的渡河,此种情况下渡河时间最短,但是渡河位移不是最短;
关于渡河问题,还要会判断能否垂直渡河,其条件是船在静水中的速度大小要大于河水流动的速度大小.

 每课必练系列答案
每课必练系列答案| A. | 质量越大,离地面越远,速度越大 | |
| B. | 与质量无关,离地面越近,速度越大 | |
| C. | 人造卫星的运行速度大于等于7.9 km/s | |
| D. | 人造卫星的发射速度等于7.9 km/s |
 如图所示,从地面上方某点,将一小球以10m/s的初速度沿水平方向抛出,小球经过1s落地,不计空气阻力(g=10m/s2),求:
如图所示,从地面上方某点,将一小球以10m/s的初速度沿水平方向抛出,小球经过1s落地,不计空气阻力(g=10m/s2),求:(1)小球从抛出点到落地点的水平位移大小
(2)小球落地时的速度大小.
 一个内壁光滑的圆锥形筒的轴线垂直于水平面,圆锥筒固定,有质量相同的小球A和B沿着筒的内壁在水平面内做匀速圆周运动,如图所示,A的运动半径较大,则( )
一个内壁光滑的圆锥形筒的轴线垂直于水平面,圆锥筒固定,有质量相同的小球A和B沿着筒的内壁在水平面内做匀速圆周运动,如图所示,A的运动半径较大,则( )| A. | 球A的角速度必大于球B的角速度 | |
| B. | 球A的线速度必大于球B的线速度 | |
| C. | 球A的运动周期必大于球B的运动周期 | |
| D. | 球A对筒壁的压力必大于球B对筒壁的压力 |
| A. | 因为是地球的同步卫星,所以在轨道上的运行速度与赤道上某点的线速度大小相等 | |
| B. | 因为是地球的同步卫星,所以它的角速度与赤道上某点的角速度大小相等 | |
| C. | 其轨道速度大于7.9km/s | |
| D. | 根据需要可以把同步卫星定点在中山上空 |
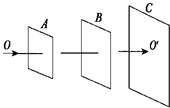 在如图所示中,A、B为两偏振片,一束自然光沿OO′方向射向A,此时在光屏C上,透射光的强度最大,则下列说法中正确的是( )
在如图所示中,A、B为两偏振片,一束自然光沿OO′方向射向A,此时在光屏C上,透射光的强度最大,则下列说法中正确的是( )| A. | 此时A,B的偏振方向平行 | |
| B. | 只有将B绕OO′轴顺时针旋转90°,屏上透射光的强度最弱,几乎为零 | |
| C. | 不论将A或B绕OO′轴旋转90°时,屏上透射光的强度最弱,几乎为零 | |
| D. | 将A沿顺时针方向旋转180°时,屏上透射光的强度最弱,几乎为零 |
 如图所示,小球A质量为m,固定在长为L的轻细直杆一端,并随杆一起绕杆的另一端O点在竖直平面内做圆周运动,如果小球经过最高位置时速度为$\sqrt{2gl}$,则杆对球的作用力为( )
如图所示,小球A质量为m,固定在长为L的轻细直杆一端,并随杆一起绕杆的另一端O点在竖直平面内做圆周运动,如果小球经过最高位置时速度为$\sqrt{2gl}$,则杆对球的作用力为( )| A. | 推力,2mg | B. | 拉力,2mg | C. | 推力,mg | D. | 拉力,mg |
 如图所示,飞机距离地面高H=500m,水平飞行速度为v1=100m/s,追击一辆速度为v2=15m/s同向行驶的汽车,欲使投弹击中汽车,飞机应在距汽车水平距离多远处投弹?(g=10m/s2)
如图所示,飞机距离地面高H=500m,水平飞行速度为v1=100m/s,追击一辆速度为v2=15m/s同向行驶的汽车,欲使投弹击中汽车,飞机应在距汽车水平距离多远处投弹?(g=10m/s2)