题目内容
12.关于地球同步卫星,下列说法正确的是( )| A. | 因为是地球的同步卫星,所以在轨道上的运行速度与赤道上某点的线速度大小相等 | |
| B. | 因为是地球的同步卫星,所以它的角速度与赤道上某点的角速度大小相等 | |
| C. | 其轨道速度大于7.9km/s | |
| D. | 根据需要可以把同步卫星定点在中山上空 |
分析 人造地球卫星的轨道必须通过地心;卫星运行时,由地球的万有引力提供向心力,有牛顿第二定律列方程列关于线速度、周期等的表达式分析即可.地球同步卫星的周期等于地球自转的周期,并根据发射速度与环绕速度的区别来分析求解.
解答 解:A、根据v=ωr,虽然它们的角速度相同,但它们的半径不同,则同步卫星在轨道上的运行速度比赤道上某点的线速度大,故A错误.
B、因为是地球的同步卫星,所以它的角速度与赤道上某点的角速度大小相等,故B正确;
C、根据$\frac{GMm}{{r}^{2}}$=m$\frac{{v}^{2}}{r}$,可知,当轨道半径越大时,线速度越小,则卫星的运行速度小于7.9km/s.故C错误.
D、同步卫星只能在赤道的正上方,它若在除赤道所在平面外的任意点,假设实现了“同步”,那它的运动轨道所在平面与受到地球的引力就不在一个平面上,这是不可能的,所以不可能定点在中山正上方,故D错误.
故选:B.
点评 本题关键掌握卫星问题的基本思路:万有引力等于向心力,知道地球同步卫星的四个“定”:定轨道、定高度、定速度、定周期,属于基础题.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案
相关题目
2.摆长为l的单摆,上端悬线固定,把摆球从平衡位置拉开一小段距离,使摆线与竖直方向的夹角小于5°然后无初速地释放.摆球运动到平衡位置时所需时间为t1.若把摆球托到悬点位置,让其自由下落,运动到平衡位置所需时间为t2.不计空气阻力,则有( )
| A. | t1>t2 | B. | t1<t2 | C. | t1=t2 | D. | 不能确定 |
20. 如图所示,在同一轨道平面上,有绕地球做匀速圆周运动的卫星A、B、C,下列说法正确的是( )
如图所示,在同一轨道平面上,有绕地球做匀速圆周运动的卫星A、B、C,下列说法正确的是( )
 如图所示,在同一轨道平面上,有绕地球做匀速圆周运动的卫星A、B、C,下列说法正确的是( )
如图所示,在同一轨道平面上,有绕地球做匀速圆周运动的卫星A、B、C,下列说法正确的是( )| A. | A的线速度最小 | B. | B的角速度最小 | ||
| C. | C周期最长 | D. | A的向心加速度最小 |
17. 如图所示是双缝干涉实验装置,使用波长为600nm的橙色光源照射单缝S,在光屏中央P处观察到亮条纹,在位于P点上方的P1点出现第一条亮纹中心(即P1到S1、S2的光程差为一个波长),现换用波长为400nm的紫光源照射单缝( )
如图所示是双缝干涉实验装置,使用波长为600nm的橙色光源照射单缝S,在光屏中央P处观察到亮条纹,在位于P点上方的P1点出现第一条亮纹中心(即P1到S1、S2的光程差为一个波长),现换用波长为400nm的紫光源照射单缝( )
 如图所示是双缝干涉实验装置,使用波长为600nm的橙色光源照射单缝S,在光屏中央P处观察到亮条纹,在位于P点上方的P1点出现第一条亮纹中心(即P1到S1、S2的光程差为一个波长),现换用波长为400nm的紫光源照射单缝( )
如图所示是双缝干涉实验装置,使用波长为600nm的橙色光源照射单缝S,在光屏中央P处观察到亮条纹,在位于P点上方的P1点出现第一条亮纹中心(即P1到S1、S2的光程差为一个波长),现换用波长为400nm的紫光源照射单缝( )| A. | P和P1仍为亮点 | B. | P为亮点,P1为暗点 | ||
| C. | P为暗点,P1为亮点 | D. | P、P1均为暗点 |
2.关于曲线运动,下列说法正确的有( )
| A. | 做曲线运动的物体,加速度一定是变化的 | |
| B. | 加速度和速度数值均不变的运动是直线运动 | |
| C. | 做曲线运动的物体一定具有加速度 | |
| D. | 物体在恒力作用下,不可能做曲线运动 |
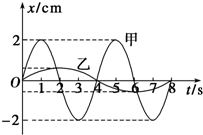 如图所示是两个单摆的振动图象.
如图所示是两个单摆的振动图象.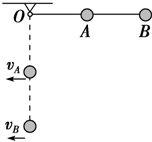 如图所示,在长为L的轻杆中点A和端点B各固定一质量为m的小球(可看做质点),杆可绕无摩擦的轴O转动,使杆从水平位置无初速度释放摆下,重力加速度为g.当杆转到竖直位置时:
如图所示,在长为L的轻杆中点A和端点B各固定一质量为m的小球(可看做质点),杆可绕无摩擦的轴O转动,使杆从水平位置无初速度释放摆下,重力加速度为g.当杆转到竖直位置时: