题目内容
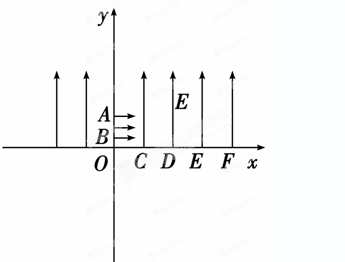
(13分) 如图所示,足够长的光滑导轨ab、cd固定在竖直平面内,导轨间距为d,b、c两点间接一阻值为r的电阻。ef是一水平放置的导体杆,其质量为m、有效电阻值为r,杆与ab、cd保持良好接触。整个装置放在磁感应强度大小为B的匀强磁场中,磁场方向与导轨平面垂直。现用一竖直向上的力拉导体杆,使导体杆从静止开始做加速度为 的匀加速运动,上升了H高度,这一过程中bc间电阻r产生的焦耳热为Q,g为重力加速度,不计导轨电阻及感应电流间的相互作用。求:
的匀加速运动,上升了H高度,这一过程中bc间电阻r产生的焦耳热为Q,g为重力加速度,不计导轨电阻及感应电流间的相互作用。求:

⑴导体杆上升到H过程中通过杆的电量;
⑵导体杆上升到H时所受拉力F的大小;
⑶导体杆上升到H过程中拉力做的功。
 的匀加速运动,上升了H高度,这一过程中bc间电阻r产生的焦耳热为Q,g为重力加速度,不计导轨电阻及感应电流间的相互作用。求:
的匀加速运动,上升了H高度,这一过程中bc间电阻r产生的焦耳热为Q,g为重力加速度,不计导轨电阻及感应电流间的相互作用。求:
⑴导体杆上升到H过程中通过杆的电量;
⑵导体杆上升到H时所受拉力F的大小;
⑶导体杆上升到H过程中拉力做的功。
(1)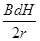 (2)
(2)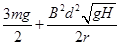 (3)
(3)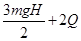
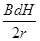 (2)
(2)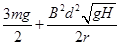 (3)
(3)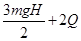
试题分析:(1)导体杆上升到H过程中,回路面积减小,磁通量变化产生感应电动势,根据电磁感应定律得:
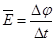
根据闭合电路的欧姆定律得:感应电流平均值

通过杆的感应电量为
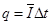
以上各式联立解得:导体杆上升到H过程中通过杆的电量
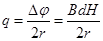
(2)设ef上升到H时,速度为
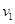 、拉力为F、感应电流瞬时值为
、拉力为F、感应电流瞬时值为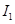 ,根据运动学公式得:
,根据运动学公式得: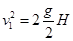 解得
解得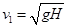
根据牛顿第二定律,得
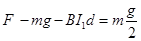
根据闭合电路的欧姆定律,得
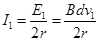
综上三式,联立解得导体杆上升到H时所受拉力F的大小
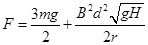
(3)导体杆上升到H过程中,安培力做负功,由功能关系知克服安培力做功为回路产生的电热的2倍,即
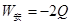 .
.由功能关系得:
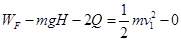
解得:
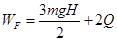

练习册系列答案
相关题目




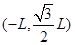 ,带电粒子质量为m,电荷量为q,初速度为v0,不计粒子重力。求:
,带电粒子质量为m,电荷量为q,初速度为v0,不计粒子重力。求: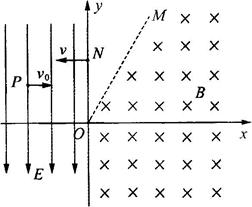

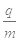 =5×104C/kg,不计粒子的重力。求:
=5×104C/kg,不计粒子的重力。求: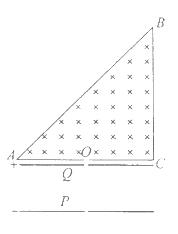
 L。现在一群质量为m、电荷量大小为q(重力不计)的带电粒子,分布在A、B之间。t=0时刻,这群带电粒子以相同的初速度v0沿x轴正方向开始运动。观察到从A点出发的带电粒子恰好从D点第一次进入磁场,然后从O点第一次离开磁场。
L。现在一群质量为m、电荷量大小为q(重力不计)的带电粒子,分布在A、B之间。t=0时刻,这群带电粒子以相同的初速度v0沿x轴正方向开始运动。观察到从A点出发的带电粒子恰好从D点第一次进入磁场,然后从O点第一次离开磁场。