题目内容
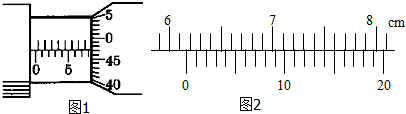
8.在用落体法验证机械能守恒定律时,某同学按照正确的操作选得纸带如右.其中O是起始点,A、B、C是打点计时器连续打下的3个点.该同学用毫米刻度尺测量O到A、B、C各点的距离,并记录在图中(单位cm).
(1)这三个数据中不符合有效数字读数要求的是15.7,应记作15.70cm.
(2)该同学用重锤在OB段的运动来验证机械能守恒,已知当地的重力加速度g=9.80m/s2,他用AC段的平均速度作为跟B点对应的物体的即时速度,则该段重锤重力势能的减少量为1.22m,而动能的增加量为1.20m,(均保留3位有效数字,重锤质量用m表示).这样验证的系统误差总是使重力势能的减少量大于动能的增加量,原因是在重锤下落过程中由于摩擦生热,机械能有损失,减少的重力势能一部分转化为内能..
(3)另一位同学根据同一条纸带,同一组数据,也用重锤在OB段的运动来验证机械能守恒,不过他数了一下:从打点计时器打下的第一个点O数起,图中的B是打点计时器打下的第9个点.因此他用vB=gt计算跟B点对应的物体的即时速度,得到动能的增加量为1.23m,这样验证时的系统误差总是使重力势能的减少量小于动能的增加量,原因是式中用g=9.8m/s2计算,而实际上重锤下落的加速度小于这个值.
分析 毫米刻度尺测量长度,要求估读即读到最小刻度的下一位.纸带法实验中,若纸带匀变速直线运动,测得纸带上的点间距,利用匀变速直线运动的推论,可计算出打出某点时纸带运动的瞬时速度,从而求出动能.根据功能关系得重力势能减小量等于重力做功的数值.
解答 解:(1)由图中信息可知,测量所用的刻度尺的最小分度是毫米,因此按有效数字的读数要求,应读到毫米的十分位上,故图中 OC段数据不合要求,应读作15.70.
(2)重力势能的减小量△EP=mghB=m×9.80×0.1242=1.22m,B点的速度为:
${v}_{B}=\frac{{x}_{AC}}{2T}=\frac{0.157-0.0951}{2×0.02}m/s=1.55m/s$,
△EK=$\frac{1}{2}m{v_B}^2$=$\frac{1}{2}×m×1.5{5}^{2}$=1.20m,
由计算结果得物体重力势能的减少量 大于 物体动能的增加量.这是因为v是实际速度,在重锤下落过程中由于摩擦生热,机械能有损失,减少的重力势能一部分转化为内能.
(3)△EK=$\frac{1}{2}m{v_B}^2=\frac{1}{2}m{({gt})^2}$=1.23m,由这种方法算得的重力势能的减少量将 小于动能的增加量,这是因为v的计算值偏大,原因:式中用g=9.8m/s2计算,而实际上重锤下落的加速度小于这个值.
故答案为:(1)15.7,15.70,(2)1.22m,1.20m,大于,在重锤下落过程中由于摩擦生热,机械能有损失,减少的重力势能一部分转化为内能.
(3)1.23m,小于,式中用g=9.8m/s2计算,而实际上重锤下落的加速度小于这个值.
点评 纸带问题的处理时力学实验中常见的问题.我们可以纸带法实验中,若纸带匀变速直线运动,测得纸带上的点间距,利用匀变速直线运动的推论,可计算出打出某点时纸带运动的瞬时速度和加速度,这是纸带法实验中考查的重点.

 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案 如图所示,质量相同的两个带电粒子P、Q以相同的速度沿垂直于电场方向射入两平行板间的匀强电场中,P从两极板正中央射入,Q从下极板边缘处射入,它们最后打在同一点(重力不计),则从开始射入到打到上板的过程中( )
如图所示,质量相同的两个带电粒子P、Q以相同的速度沿垂直于电场方向射入两平行板间的匀强电场中,P从两极板正中央射入,Q从下极板边缘处射入,它们最后打在同一点(重力不计),则从开始射入到打到上板的过程中( )| A. | 它们运动的时间tQ>tP | |
| B. | 它们运动的加速度aQ<aP | |
| C. | 它们的动能增加量之比△EkP:△EkQ=1:4 | |
| D. | 它们所带的电荷量之比qP:qQ=2:1 |
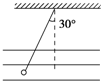 如图所示,一个质量为30g、带电量为-1.7×10-8C的半径极小的小球用丝线悬挂在某匀强电场中,电场线与水平面平行.当小球静止时,测得悬线与竖直方向夹角为30°,则匀强电场方向和大小为(g取10m/s2)( )
如图所示,一个质量为30g、带电量为-1.7×10-8C的半径极小的小球用丝线悬挂在某匀强电场中,电场线与水平面平行.当小球静止时,测得悬线与竖直方向夹角为30°,则匀强电场方向和大小为(g取10m/s2)( )| A. | 水平向右5×106N/C | B. | 水平向右1×107 N/C | ||
| C. | 水平向左5×106N/C | D. | 水平向左1×107N/C |
 如图所示,一理想变压器原线圈匝数为n1=1000匝,副线圈匝数为n2=200匝,将原线圈接在u=200$\sqrt{2}$sin100πt(V)的交流电压上,副线圈上电阻R和理想交流电压表并联接入电路,现在A、B两点间接入不同的电子元件,则下列说法正确的是( )
如图所示,一理想变压器原线圈匝数为n1=1000匝,副线圈匝数为n2=200匝,将原线圈接在u=200$\sqrt{2}$sin100πt(V)的交流电压上,副线圈上电阻R和理想交流电压表并联接入电路,现在A、B两点间接入不同的电子元件,则下列说法正确的是( )| A. | 在A、B两点间串联一只电阻R,穿过铁芯的磁通量的最大变化率为0.2Wb/s | |
| B. | 在A、B两点间接入理想二极管,电压表读数为40V | |
| C. | 在A、B两点间接入一只电容器,只提高交流电频率,电压表读数增大 | |
| D. | 在A、B两点间接入一只电感线圈,只提高交流电频率,电阻R消耗电功率减小 |
 如图所示,离地H高处有一个质量为m、带电量为+q的物体处于电场强度随时间变化规律为E=E0-kt(E0、k均为大于零的常数,电场水平向左为正方向)的电场中,物体与竖直绝缘墙壁间的动摩擦因数为μ,已知μqE0>mg.t=0时,物体从墙上静止释放,若物体所受的最大静摩擦力等于滑动摩擦力,当物体下滑$\frac{H}{2}$后脱离墙面,此时速度大小为$\frac{\sqrt{gH}}{2}$,最终落在地面上.则下列关于物体的运动说法正确的是( )
如图所示,离地H高处有一个质量为m、带电量为+q的物体处于电场强度随时间变化规律为E=E0-kt(E0、k均为大于零的常数,电场水平向左为正方向)的电场中,物体与竖直绝缘墙壁间的动摩擦因数为μ,已知μqE0>mg.t=0时,物体从墙上静止释放,若物体所受的最大静摩擦力等于滑动摩擦力,当物体下滑$\frac{H}{2}$后脱离墙面,此时速度大小为$\frac{\sqrt{gH}}{2}$,最终落在地面上.则下列关于物体的运动说法正确的是( )| A. | 物体克服摩擦力所做的功W=$\frac{3}{8}$mgH | |
| B. | 物体与墙壁脱离的时刻为t=$\frac{{E}_{0}}{k}$ | |
| C. | 当物体沿墙壁下滑时,物体先加速再做匀速直线运动 | |
| D. | 物体从脱离墙壁到落地之前的运动轨迹是一段直线 |
| A. | 两小球运动时间相同 | B. | 重力对两小球的冲量相同 | ||
| C. | 两小球着地时的动量相同 | D. | 两小球着地时的动能相同 |

 为测量一直流电源的电动势及内阻
为测量一直流电源的电动势及内阻