题目内容
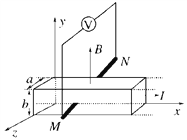
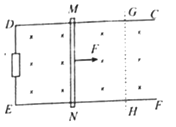
【题目】如图所示,固定于水平面上的足够长的金属框架CDEF处在竖直向下的匀强磁场中,磁感应强度B0=2T,柜架的左端串有阻值为R=5Ω的定值电阻,框架的宽度L=0.5m,质量m=0.05kg,电阻不计的金属棒MN与导轨垂直并良好接触,金属棒与导轨之间的动摩擦因数μ=0.5,金属棒在F=0.5N的水平恒力作用下由静止开始沿框架向右运动,最后达到稳定速度。重力加速度大小为g,导轨的电阻不计。求:
(1)金属棒开始运动瞬间的加速度大小;
(2)金属棒达到的稳定速度大小;
(3)金属棒达到稳定速度后,某时刻的位置GH到框架左端的距离为x=7.5m,并将该时刻记作t=0,从此时刻起,让磁感应强度逐渐减小,使金属棒中不产生感应电流,则t=2s时磁感应强度B为多大?
【答案】(1)5m/s2;(2)1.25m/s;(3)1.5T。
【解析】
(1)金属棒开始运动瞬间安培力为零,金属棒水平方向受到拉力和摩擦力,根据牛顿第二定律可得
F-μmg=ma
解得:
a=5m/s2;
(2)金属棒达到稳定时受力平衡,水平方向受到拉力、摩擦力和安培力作用。根据平衡条件可得:
F=μmg+B0IL
其中![]() 解得
解得
![]()
代入数据解得:
v=1.25m/s;
(3)金属棒达到稳定速度后,某时刻的位置GH到框架左端的距离为x=7.5m,并将该时刻记作t=0,则该时刻的磁通量为:
Φ1=B0Lx
则t时的磁通量
Φ2=BL(x+vt)
金属棒中不产生感应电流,则有
Φ1=Φ2
解得
![]()
当t=2s时
![]()

 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案【题目】通过实验测绘一个标有“3V,![]() ”的小灯泡的伏安特性曲线,灯泡两端的电压需要由零逐渐增加到3V;实验中除
”的小灯泡的伏安特性曲线,灯泡两端的电压需要由零逐渐增加到3V;实验中除![]() 的电源;开关;导线若干外,还备有以下器材:
的电源;开关;导线若干外,还备有以下器材:
A.电流表:量程![]() ,内阻1Ω;
,内阻1Ω;
B.电流表:量程![]() ,内阻0.3Ω;
,内阻0.3Ω;
C.电压表(量程![]() ,内阻约
,内阻约![]() );
);
D.电压表(量程![]() ,内阻约
,内阻约![]() );
);
E.滑动变阻器(阻值![]() );
);
F.滑动变阻器(阻值![]() );
);
(1)为了测量准确,实验中应选用电流表______,电压表______,滑动变阻器______(填序号)。
(2)在本实验中,滑动变阻器应采用______(“分压”或“限流”)填接法,电流表应采用______(填“内”或“外”)接法,如果用实验所测数据来求电阻,则测量结果比真实数值要______(选填“大”或“小”)。
(3)某同学在实验中得到如下一组U和I的数据:
编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
U/V |
|
|
|
|
|
|
|
|
I/A |
|
|
|
|
|
|
|
|
①在图上画出![]() 图线_______________。
图线_______________。
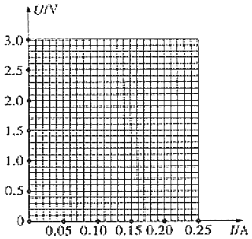
②从图线上可以看出,当功率逐渐增大时,灯丝电阻的变化情况是______(增大、减小);这表明导体的电阻随温度升高而______(升高、降低)。