题目内容
发射一月球探测器绕月球做匀速圆周运动，测得探测器在离月球表面高度分别为h1和h2的圆轨道上运动时，周期分别为T1和T2。设想月球可视为质量分布均匀的球体，万有引力常量为G。仅利用以上数据，可以计算出（ ）
| A．月球的质量 | B．探测器的质量 |
| C．月球的密度 | D．探测器在离月球表面高度为h1的圆轨道上运动时的加速度犬小 |
ACD
解析试题分析：根据万有引力提供向心力
，
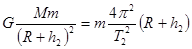，联立可求月舞的质量M、月球的半径R，再根据
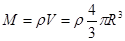，可求月球的密度，探测器的质量无法求出，探测器在离月球表面高度为h1的圆轨道上运动时的加速度
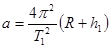也可求出，所以A、C、D正确；B错误。
考点：本题考查天体运动
天天向上一本好卷系列答案
小学生10分钟应用题系列答案下列说法中正确的是（ ）
| A．两质点间万有引力为F，当它们间的距离增加一倍时，它们之间的万有引力是F/2 |
| B．树上的苹果掉到地上，这说明地球吸引苹果的力大于苹果吸引地球的力 |
C．由万有引力公式 可知，当其他条件不变而r趋近0时，F趋于无穷大 |
| D．万有引力常量最先由英国物理学家卡文迪许通过扭称实验准确测得 |
“嫦娥三号”探月飞行器在100km的环月近圆轨道和落月前的15km轨道飞行时，若均视为匀速圆周运动，则
| A．“嫦娥三号”在100km轨道比在15km轨道上运行的周期短 |
| B．“嫦娥三号”在100km轨道比在15km轨道上运行的线速度大 |
| C．“嫦娥三号”在100km轨道比在15km轨道上运行的角速度大 |
| D．“嫦娥三号”在100km轨道比在15km轨道上运行的向心加速度小 |
某国际研究小组观测到了一组双星系统，它们绕二者连线上的某点做匀速圆周运动，双星系统中质量较小的星体能“吸食”质量较大的星体的表面物质，达到质量转移的目的．根据大爆炸宇宙学可知，双星间的距离在缓慢增大，假设星体的轨道近似为圆，则在该过程中（ ）
| A．双星做圆周运动的角速度不断减小 |
| B．双星做圆周运动的角速度不断增大 |
| C．质量较大的星体做圆周运动的轨道半径渐小 |
| D．质量较大的星体做圆周运动的轨道半径增大 |
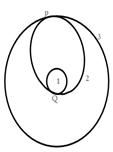
2013年12月11日，“嫦娥三号”从距月面高度为100km的环月圆轨道Ⅰ上的P点实施变轨，进入近月点为15km的椭圆轨道Ⅱ，由近月点Q成功落月，如图所示。关于“嫦娥三号”，下列说法正确的是
| A．沿轨道Ⅰ运动至P时，需制动减速才能进入轨道Ⅱ |
| B．沿轨道Ⅱ运行的周期大于沿轨道Ⅰ运行的周期 |
| C．沿轨道Ⅱ运行时，在P点的加速度大于在Q点的加速度 |
| D．在轨道Ⅱ上由P点运行到Q点的过程中，万有引力对其做负功 |
北京时间2013年12月10日晚上九点二十分，在太空飞行了九天的“嫦娥三号”飞船，再次成功变轨，从100km的环月圆轨道Ⅰ，降低到近月点15km、远月点100km的椭圆轨道Ⅱ，两轨道相交于点P，如图所示。关于“嫦娥三号”飞船，以下说法不正确的是（ ）
| A．在轨道Ⅰ上运动到P点的速度比在轨道Ⅱ上运动到P点的速度大 |
| B．在轨道Ⅰ上P点的向心加速度比在轨道Ⅱ上运动到P点的向心加速度小 |
| C．在轨道Ⅰ上的势能与动能之和比在轨道Ⅱ上的势能与动能之和大 |
| D．在轨道Ⅰ上运动的周期大于在轨道Ⅱ上运动的周期 |
设地球的半径为R，地球表面重力加速度为g，月球绕地球公转周期为T，玉兔号月球车所拍摄的月面照片从月球以电磁波形式发送到北京航天飞行控制中心所用时间约为（真空中的光速为c，月地距离远大于地球半径）（ ）
A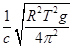． | B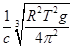． | C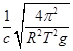． | D． |
a、b、c、d是在地球大气层外的圆形轨道上运行的四颗人造卫星．其中a、c的轨道相交于P，b、d在同一个圆轨道上．b、c轨道在同一平面上．某时刻四颗卫星的运行方向及位置如图所示．下列说法中正确的是
| A．a、c的加速度大小相等，且大于b的加速度 |
| B．b、c的角速度大小相等，且小于a的角速度 |
| C．a、c的线速度大小相等，且小于d的线速度 |
| D．a、c存在P点相撞的危险 |
