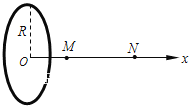Question

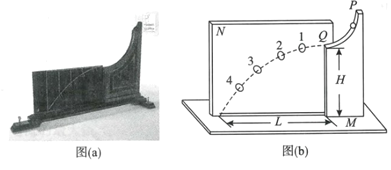
【题目】如图（a）所示是伽利略研究平抛运动的实验装置，现收藏于伽利略博物馆，其装置可简化为如图（b）所示。图（b）中水平放置的底板上竖直地固定有M板和N板。M板上部有一半径为R的圆弧形的粗糙轨道，P为最高点，Q为最低点，Q点处的切线水平，距底板高为H。先将小铜球从P处静止释放，测出小球在底板上的落点到Q点的水平距离为L，然后将4个圆环固定在N板上的适当位置（相邻两圆环的水平距离均为），使得小铜球从P处静止释放后可无阻碍地通过各圆环中心，则（　　）

A.四个圆环离地的高度之比为16:9:4:1

B.小铜球依次经过4个圆环时的竖直方向的速度之比为1:3:5:7

C.第1、2两个圆环的高度差为

D.第1、3两个圆环的高度差为

Answer 1

【答案】C

【解析】

A．根据题意，相邻两圆环的水平距离均为，则四个圆环间隔时间差相等且为总时间的，设下落的总时间为t，则

第一个圆环离地高度为

第二个圆环离地高度为

第三个圆环离地高度为

第四个圆环离地高度为

所以

故A错误；

B．第一个圆环竖直方向的速度为

第二个圆环竖直方向的速度为

第三个圆环竖直方向的速度为

第四个圆环竖直方向的速度为

解得

故B错误；

C．第1、2两个圆环的高度差为

故C正确；

D．第1、3两个圆环的高度差为

故D错误。

故选C。