��Ŀ����
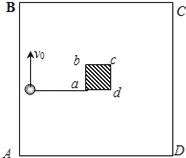
����Ŀ����ͼ��ʾ���ڹ⻬ˮƽ����ABCD����̶���һ�߳�Ϊ0.4m�⻬С����abcd����ΪL=1m��ϸ�ߣ�һ��˩��a�ϣ���һ��˩סһ������Ϊm=0.5kg��С��С��ij�ʼλ����ad������a��һ�࣬��ϸ����ֱ������С����v0=2m/s�Ĵ�ֱ��ϸ�߷����ˮƽ�ٶ�ʹ����Բ���˶������ڹ⻬С����abcd�Ĵ��ڣ�ʹ������abcd�ϣ���ϸ���ܳ��ܵ��������Ϊ7N���������ܵ��������ڻ����7Nʱ�������Ͽ�������ô�ӿ�ʼ�˶���ϸ�߶���Ӧ�����ʱ�䣿С����������һ�߷������棿
���𰸡�1.256s��AD����
���������赱�߳�ΪL0ʱ���߽����ѣ�������������ʽ��T��![]() ������L0��0.29 m.
������L0��0.29 m.
��a��ת![]() �ܵ�ʱ��
�ܵ�ʱ��
t1��![]() ��
��![]() ��0.785 s��
��0.785 s��
��b��ת![]() �ܵ�ʱ��
�ܵ�ʱ��
t2��![]() ��
��![]() ��0.471 s��
��0.471 s��
�߽Ӵ�c���С����Բ���˶��İ뾶Ϊr��0.2 m��С��L0��0.29 m���������������ѣ�
���Դӿ�ʼ�˶����߶��Ѿ���t��1.256 s��С��������AD�߷������森

��ϰ��ϵ�д�
�����Ŀ





