题目内容
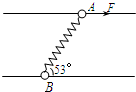如图所示，A、B两滑环分别套在间距为1m的光滑细杆上，A和B的质量分别为1kg、3kg，用一自然长度为1m的轻弹簧将两环相连，在A环上作用一沿杆方向的、大小为20N的拉力F，当两环都沿杆以相同的加速度运动时，弹簧与杆夹角为53°（cos53°=0.6）．求：（1）弹簧的劲度系数k为多少？
（2）若突然撤去拉力F，在撤去拉力F的瞬间，A的加速度为多大？方向如何？
分析：（1）对整体分析，运用牛顿第二定律求出整体的加速度，隔离对B分析，根据牛顿第二定律求出弹簧的弹力，从而求出弹簧的劲度系数．
（2）撤去F的瞬间，弹簧的弹力不变，根据牛顿第二定律求出瞬时的加速度．
（2）撤去F的瞬间，弹簧的弹力不变，根据牛顿第二定律求出瞬时的加速度．
解答：解：（1）对AB整体分析有得：F=（mA+mB）a
对B受力分析有：k△L?cos53°=mBa
又因：△L=
-d
联立上三式代入数据得：k=100N/m
（2）撤去F瞬间对A分析，弹簧弹力不变，故：k△L?cos53°=mAa'
得：a'=15m/s2
方向水平向左．
答：（1）弹簧的劲度系数k为100N/m．
（2）撤去拉力F的瞬间，A的加速度为15m/s2，方向水平向左．
对B受力分析有：k△L?cos53°=mBa
又因：△L=
| d |
| sin530 |
联立上三式代入数据得：k=100N/m
（2）撤去F瞬间对A分析，弹簧弹力不变，故：k△L?cos53°=mAa'
得：a'=15m/s2
方向水平向左．
答：（1）弹簧的劲度系数k为100N/m．
（2）撤去拉力F的瞬间，A的加速度为15m/s2，方向水平向左．
点评：解决本题的关键能够正确地进行受力分析，通过牛顿第二定律进行求解，注意整体法和隔离法的运用．
练习册系列答案
阅读快车系列答案
相关题目
如图所示，A、B两滑块的质量均为m，分别穿在光滑的足够长的水平固定导杆上，两导杆平行，间距为d．用自然长度也为d的轻弹簧连接两滑块．开始时两滑块均处于静止状态，今给滑块B一个向右的瞬时冲量I，则以后滑块A的最大速度为（ ）
如图所示，A与B两滑块叠放在水平面上，已知A与B所受重力分别为GA=10N，GB=20N，A与B间的动摩擦因数μA=0.4，B与水平面间的动摩擦因数μB=0.3，试求在图（a）和图（b）所示的两种情况下拉动滑块B所需的最小拉力分别为多大？（设最大静摩擦力等于滑动摩擦力）
（2011?辽宁二模）（1）下列说法正确的是