题目内容
 如图所示,A、B两滑块的质量均为m,分别穿在光滑的足够长的水平固定导杆上,两导杆平行,间距为d.用自然长度也为d的轻弹簧连接两滑块.开始时两滑块均处于静止状态,今给滑块B一个向右的瞬时冲量I,则以后滑块A的最大速度为( )
如图所示,A、B两滑块的质量均为m,分别穿在光滑的足够长的水平固定导杆上,两导杆平行,间距为d.用自然长度也为d的轻弹簧连接两滑块.开始时两滑块均处于静止状态,今给滑块B一个向右的瞬时冲量I,则以后滑块A的最大速度为( )分析:解答本题需掌握(1)动量定理:合外力的冲量等于物体动量的变化;(2)系统水平方向不受外力,则系统在水平方向上动量守恒,系统的机械能守恒;(3)A物体速度最大时即动量最大,此时B物体速度最小也就是弹簧恢复原长时有最大值.
解答:解:弹簧恢复原长时A的速度最大,设此速度为vm,设此时B的速度为
,B物体获得的初速度为vB
根据动量定理,给滑块B的一个冲量I=mvB-0
∴vB=
B获得冲量后,A、B弹簧组成的系统动量和机械能均守恒,则得:
mvB=mvm+m
(1)
m
=
m
+
m
2 (2)
联列(1)和(2)式可解得vm=vB=
故选B
| v | ′ B |
根据动量定理,给滑块B的一个冲量I=mvB-0
∴vB=
| I |
| m |
B获得冲量后,A、B弹簧组成的系统动量和机械能均守恒,则得:
mvB=mvm+m
| v | ′ B |
| 1 |
| 2 |
| v | 2 B |
| 1 |
| 2 |
| v | 2 m |
| 1 |
| 2 |
| v | ′ B |
联列(1)和(2)式可解得vm=vB=
| I |
| m |
故选B
点评:本题通过系统的动量守恒和机械能守恒以及动理定理的应用,需要学生一定的知识综合能力,找到最大值的条件即可.学生碰到这类问题一般难易下手.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
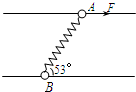 如图所示,A、B两滑环分别套在间距为1m的光滑细杆上,A和B的质量分别为1kg、3kg,用一自然长度为1m的轻弹簧将两环相连,在A环上作用一沿杆方向的、大小为20N的拉力F,当两环都沿杆以相同的加速度运动时,弹簧与杆夹角为53°(cos53°=0.6).求:
如图所示,A、B两滑环分别套在间距为1m的光滑细杆上,A和B的质量分别为1kg、3kg,用一自然长度为1m的轻弹簧将两环相连,在A环上作用一沿杆方向的、大小为20N的拉力F,当两环都沿杆以相同的加速度运动时,弹簧与杆夹角为53°(cos53°=0.6).求: 如图所示,A与B两滑块叠放在水平面上,已知A与B所受重力分别为GA=10N,GB=20N,A与B间的动摩擦因数μA=0.4,B与水平面间的动摩擦因数μB=0.3,试求在图(a)和图(b)所示的两种情况下拉动滑块B所需的最小拉力分别为多大?(设最大静摩擦力等于滑动摩擦力)
如图所示,A与B两滑块叠放在水平面上,已知A与B所受重力分别为GA=10N,GB=20N,A与B间的动摩擦因数μA=0.4,B与水平面间的动摩擦因数μB=0.3,试求在图(a)和图(b)所示的两种情况下拉动滑块B所需的最小拉力分别为多大?(设最大静摩擦力等于滑动摩擦力) (2011?辽宁二模)(1)下列说法正确的是
(2011?辽宁二模)(1)下列说法正确的是