��Ŀ����
 ��2011?������ģ����1������˵����ȷ����
��2011?������ģ����1������˵����ȷ����BCD
BCD
��������ȷѡ��ǰ����ĸ��A���ں˵�վ������ʯī���ش����ͨˮ��������ʽ��Ӧ�ٶ�
B���еȴ�С�ĺ˵ıȽ������������Щ�������ȶ���
C��ԭ�ӵ������Dz������ģ�ֻ��ȡһϵ�в���������
D����Ȼ��������ķ��ֽ�ʾ��ԭ�Ӻ˾��и��ӵĽṹ
��2����ͼ��ʾ��a��b�����������ֱ�Ϊm1��m2��m1��m2�����ֱ�����ˮƽ�⻬�����ϣ�ab֮���������ʵ��ɣ����ɵ���Ȼ�����뵼�˼������Ⱦ�Ϊd�������㹻������ʼʱab��ͬһ��ֱ���ϣ��Ҵ��ھ�ֹ״̬���ָ�bһ��ˮƽ����I���Դ˺���
��a�����ܴﵽ������ٶ�Ϊ���٣�
�����������������ʱ������a���ٶȴ�СΪ���٣�
��������1����ȷ�������Ҫ���գ��˵�վ����ο��Ʒ�Ӧ�ٶȣ��Ƚ���ܵ��������壬��ȷ�������ȷ�������
��2������������բٶ����������������ij����������嶯���ı仯����ϵͳˮƽ��������������ϵͳ��ˮƽ�����϶����غ㣬ϵͳ�Ļ�е���غ㣮
��2������������բٶ����������������ij����������嶯���ı仯����ϵͳˮƽ��������������ϵͳ��ˮƽ�����϶����غ㣬ϵͳ�Ļ�е���غ㣮
����⣺��1��A���ں˵�վ�У�ͨ�����ư���һ����ʯī�����������Ӷ��������Ʒ�Ӧ�ٶȣ���A����
B���Ƚ����Խ��ʾԭ�Ӻ��к��ӽ�ϵ�Խ�ι̣�ԭ�Ӻ�Խ�ȶ����еȴ�С�ĺ˵ıȽ�������������Щ�������ȶ��ģ���B��ȷ��
C��ԭ�ӵ������Dz������ģ�ֻ��ȡһϵ�в�������������C��ȷ
D��������ʶ��ԭ�Ӻ��и��ӵĽṹ�Ǵ���Ȼ��������ʼ�ģ���D��ȷ��
��ѡBCD
��2���٣����ɻָ�ԭ��ʱa���ٶ��������ٶ�Ϊv1����ʱb���ٶ�Ϊv2
���ݶ���������������b��һ������
I=m2v0-0
b��ó�����a��b������ɵ�ϵͳ�����ͻ�е�ܾ��غ㣬��ã�
m2v0=m2v2+m1v1
=
+
���v1=
�����������������ʱ����������ٶ���ȣ����ʱ�ٶ�Ϊv
����ϵͳ�����غ��
m2v0=��m2+m1��v
v=
�ʴ�Ϊ����1��BCD
��2����a�����ܴﵽ������ٶ�Ϊ
�����������������ʱ������a���ٶȴ�СΪ
��
B���Ƚ����Խ��ʾԭ�Ӻ��к��ӽ�ϵ�Խ�ι̣�ԭ�Ӻ�Խ�ȶ����еȴ�С�ĺ˵ıȽ�������������Щ�������ȶ��ģ���B��ȷ��
C��ԭ�ӵ������Dz������ģ�ֻ��ȡһϵ�в�������������C��ȷ
D��������ʶ��ԭ�Ӻ��и��ӵĽṹ�Ǵ���Ȼ��������ʼ�ģ���D��ȷ��
��ѡBCD
��2���٣����ɻָ�ԭ��ʱa���ٶ��������ٶ�Ϊv1����ʱb���ٶ�Ϊv2
���ݶ���������������b��һ������
I=m2v0-0
b��ó�����a��b������ɵ�ϵͳ�����ͻ�е�ܾ��غ㣬��ã�
m2v0=m2v2+m1v1
| 2 0 |
| 2 2 |
| 2 1 |
���v1=
| 2I |
| m1+m2 |
�����������������ʱ����������ٶ���ȣ����ʱ�ٶ�Ϊv
����ϵͳ�����غ��
m2v0=��m2+m1��v
v=
| I |
| m1+m2 |
�ʴ�Ϊ����1��BCD
��2����a�����ܴﵽ������ٶ�Ϊ
| 2I |
| m1+m2 |
�����������������ʱ������a���ٶȴ�СΪ
| I |
| m1+m2 |
���������⿼����ԭ�������Ļ���֪ʶ��������Щ����֪ʶҪ��ǿ�����ѵ��������߶��ڻ���֪ʶ�����⣮
Ӧ�ö����غ㶨�ɽ���Ҫע�⡰���ԡ����١�ϵͳ�ԣ��ڡ�ʸ���ԣ��ۡ�ͬʱ�ԣ��ܡ�ͬϵ�ԣ�
Ӧ�ö����غ㶨�ɽ���Ҫע�⡰���ԡ����١�ϵͳ�ԣ��ڡ�ʸ���ԣ��ۡ�ͬʱ�ԣ��ܡ�ͬϵ�ԣ�

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ
 ��2011?������ģ����ͼ��ʾ��б�����Ϊ45�㣬��б���Ϸ�A�㴦�ɾ�ֹ�ͷ�һ������Ϊm�ĵ���С����B�㴦��б����ײ����ײ���ٶȴ�С���䣬�����Ϊˮƽ������һ��ʱ����C���ٴ���б����ײ����֪AB����ĸ߶Ȳ�Ϊh���������ٶ�Ϊg�������ǿ�����������
��2011?������ģ����ͼ��ʾ��б�����Ϊ45�㣬��б���Ϸ�A�㴦�ɾ�ֹ�ͷ�һ������Ϊm�ĵ���С����B�㴦��б����ײ����ײ���ٶȴ�С���䣬�����Ϊˮƽ������һ��ʱ����C���ٴ���б����ײ����֪AB����ĸ߶Ȳ�Ϊh���������ٶ�Ϊg�������ǿ����������� ��2011?������ģ����̽�������������ٶȱ仯�Ĺ�ϵ����ʵ��װ����ͼ��ʾ��
��2011?������ģ����̽�������������ٶȱ仯�Ĺ�ϵ����ʵ��װ����ͼ��ʾ�� ��2011?������ģ���ס�����������ͬһ�ص㣬��ͬһֱ���˶������ٶ�--ʱ��ͼ����ͼ��ʾ��������
��2011?������ģ���ס�����������ͬһ�ص㣬��ͬһֱ���˶������ٶ�--ʱ��ͼ����ͼ��ʾ��������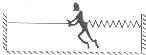 ��2011?������ģ���˶�Ա��������ͼ��ʾ��װ��ѵ�����������������Ҷ���ǽ���������ϵ���˶�Ա�����ϣ����ǽ�Ϲ̶�һ�����ӣ��ٶ�ij�˶�Ա����Ϊ50kg����������Ķ�Ħ������Ϊ��=0.2�����ɵľ���ϵ��Ϊk=1000N/m���˶�Ա˫����ס���Ӵӵ���ԭ��λ��������ǰ�����������䲻�������������˶���λ��Ϊ3mʱ���˶�Ա�ɿ����ӱ������������һ��У������Ħ�������Ƶ��ڻ���Ħ������gȡ10m/s2��������˵���в���ȷ���ǣ�������
��2011?������ģ���˶�Ա��������ͼ��ʾ��װ��ѵ�����������������Ҷ���ǽ���������ϵ���˶�Ա�����ϣ����ǽ�Ϲ̶�һ�����ӣ��ٶ�ij�˶�Ա����Ϊ50kg����������Ķ�Ħ������Ϊ��=0.2�����ɵľ���ϵ��Ϊk=1000N/m���˶�Ա˫����ס���Ӵӵ���ԭ��λ��������ǰ�����������䲻�������������˶���λ��Ϊ3mʱ���˶�Ա�ɿ����ӱ������������һ��У������Ħ�������Ƶ��ڻ���Ħ������gȡ10m/s2��������˵���в���ȷ���ǣ�������