题目内容
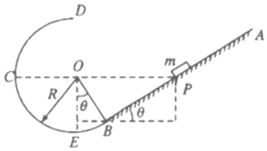
【题目】如图所示,AB是倾角为θ的粗糙直轨道,BCD是光滑的圆弧轨道,AB恰好在B点与圆弧相切,圆弧的半径为R.一个质量为m的物体(可以看作质点)从直轨道上与圆弧的圆心O等高的P点由静止释放,结果它能在两轨道间做往返运动。已知物体与轨道AB间的动摩擦因数为μ,重力加速度为g。试求:
(1)物体释放后,第一次到达B处的速度大小,并求出物体做往返运动的整个过程中在AB轨道上通过的总路程s;
(2)最终当物体通过圆弧轨道最低点E时,对圆弧轨道的压力的大小;
(3)为使物体能顺利到达圆弧轨道的最高点D(E、O、D为同一条竖直直径上的3个点),释放点距B点的距离L应满足什么条件。
【答案】(1)![]() ;
;![]() (2)
(2)![]() ; (3)
; (3)![]()
【解析】
(1)设物体释放后,第一次到达B处的速度为![]() ,根据动能定理可知:
,根据动能定理可知:
![]()
解得:
![]()
物体每完成一次往返运动,在AB斜面上能上升的高度都减少一些,最终当它达B点时,速度变为零,对物体从P到B全过程用动能定理,有
![]()
得物体在AB轨道上通过的总路程为
![]()
(2)最终物体以B为最高点在圆弧轨道底部做往返运动,设物体从B运动到E时速度为![]() v,由动能定理知:
v,由动能定理知:
![]()
在E点,由牛顿第二定律有
![]()
解得物体受到的支持力
![]()
根据牛顿第三定律,物体对轨道的压力大小为![]() ,方向竖直向下。
,方向竖直向下。
(3)设物体刚好到达D点时的速度为![]() 此时有
此时有
![]()
解得:
![]()
设物体恰好通过D点时释放点距B点的距离为![]() ,有动能定理可知:
,有动能定理可知:
![]()
联立解得:
![]()
则:
![]()
答案:(1)![]() ;
;![]() (2)
(2); (3)
![]()

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目