��Ŀ����
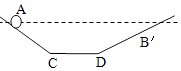
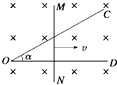
����Ŀ����ͼ��ʾ������С��Q�̶������Ϊ�ȵĹ⻬�̶���Եϸ���¶ˣ�һ����Ϊm�������Ϊq�Ĵ�����С��M���ڸ��ϴ�A���ɾ�ֹ�ͷţ�С��B��ʱ�ٶ�ǡ��Ϊ�㣬��֪A��B���ΪL��C��AB���е㣬��С�������Ϊ�ʵ㣬�������ٶ�Ϊg��������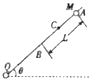
A.С���A��B�Ĺ����м��ٶ��ȼ�С������
B.С����B��ʱ�ܵ��Ŀ�������СΪmgsin��
C.С����C��ʱ�ٶ����
D.��Q�����ĵ糡�У�A��B�����ĵ��Ʋ�Ϊ�� ![]()
���𰸡�A,D
���������⣺A���������֪��С���A��ֹ�˶���B��ʱ���ٶ�Ϊ�㣬����С���ȼ��ٺ���٣���ôһ��ʼ��������С����������ϸ�˵ķ������������˶�ʱ���������������������ϸ�˵ķ�������˼��ٶ��ȼ�С��������A�������⣻
B������B��ʱ���ٶ�Ϊ�㣬�����Ǵ���ƽ��״̬��������Ҫ�����˶�����ô�ܵ��Ŀ�������С����mgsin�ȣ�B���������⣻
C������ļ��ٶ�Ϊ��ʱ���ٶȲ��ܴﵽ���C����AB���е㣬���ݿ����������ƽ���ɷ��ȣ����д˴���������֧�����������ĺ�����Ϊ�㣬�����C��ʱ�ٶȲ������C���������⣻
D�����ݶ��ܶ�������A��B�����У�0��0=mgLsin��+qUAB����ã�UAB=�� ![]() ��D�������⣻
��D�������⣻
�ʴ�Ϊ��AD��
��ϼ��ٶȺ��ٶ�֮��Ĺ�ϵ����������ٶȵ�����ʱ���ٶȳ������ֵ���ٽ��ƽ��������ţ�ٵڶ��˶����ɺͶ��ܶ����ۺ���⡣

 �������ͬ����ϰϵ�д�
�������ͬ����ϰϵ�д�