题目内容
如图甲所示,一物块在t=0时刻,以初速度v从足够长的粗糙斜面底端向上滑行,物块速度随时间变化的图象如图乙所示,t时刻物块到达最高点,3t时刻物块又返回底端.由此可以确定( )
A.物块返回底端时的速度
B.物块所受摩擦力大小
C.斜面倾角θ
D.3t时间内物块克服摩擦力所做的功
【答案】分析:速度图象与坐标轴所围“面积”等于位移,由数学知识求出位移.根据上滑与下滑的位移大小相等,可求出物块返回底端时的速度.根据动量定理分析能否求出摩擦力大小和斜面的倾角.
解答:解:A、由于下滑与上滑的位移大小相等,根据数学知识可以求出物块返回底端时的速度.设物块返回底端时的速度大小为v,则 =
=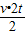 ,得到v=
,得到v=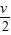 .故A正确;
.故A正确;
B、C、根据动量定理得:
上滑过程:-(mgsinθ+μmgcosθ)?t=0-mv ①
下滑过程:(mgsinθ-μmgcosθ)?2t=m ②
②
由①②解得,f=μmgcosθ=3mgsinθ-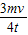 ,由于质量m未知,则无法求出f.得到sinθ=
,由于质量m未知,则无法求出f.得到sinθ=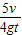 ,可以求出斜面倾角θ故B错误,C正确;
,可以求出斜面倾角θ故B错误,C正确;
D、3t时间内物块克服摩擦力所做的功等于机械能的减小量,由于物体的质量未知,故无法求解机械能减小量,无法求解克服摩擦力做的功,故D错误;
故选AC.
点评:本题抓住速度图象的“面积”等于位移分析位移和物体返回斜面底端的速度大小.也可以根据牛顿第二定律和运动学结合求解f和sinθ.
解答:解:A、由于下滑与上滑的位移大小相等,根据数学知识可以求出物块返回底端时的速度.设物块返回底端时的速度大小为v,则
 =
=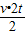 ,得到v=
,得到v=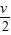 .故A正确;
.故A正确;B、C、根据动量定理得:
上滑过程:-(mgsinθ+μmgcosθ)?t=0-mv ①
下滑过程:(mgsinθ-μmgcosθ)?2t=m
 ②
②由①②解得,f=μmgcosθ=3mgsinθ-
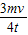 ,由于质量m未知,则无法求出f.得到sinθ=
,由于质量m未知,则无法求出f.得到sinθ=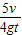 ,可以求出斜面倾角θ故B错误,C正确;
,可以求出斜面倾角θ故B错误,C正确;D、3t时间内物块克服摩擦力所做的功等于机械能的减小量,由于物体的质量未知,故无法求解机械能减小量,无法求解克服摩擦力做的功,故D错误;
故选AC.
点评:本题抓住速度图象的“面积”等于位移分析位移和物体返回斜面底端的速度大小.也可以根据牛顿第二定律和运动学结合求解f和sinθ.

练习册系列答案
相关题目
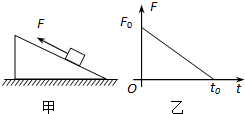 如图甲所示,一物块在粗糙斜面上,在平行斜面向上的外力F作用下,斜面和物块始终处于静止状态.当外力F按照图乙所示规律变化时,下列说法正确的是( )
如图甲所示,一物块在粗糙斜面上,在平行斜面向上的外力F作用下,斜面和物块始终处于静止状态.当外力F按照图乙所示规律变化时,下列说法正确的是( ) 如图甲所示,一物块在t=0时刻,以初速度V0从足够长的粗糙斜面底端向上滑行,物块速度随时间变化的图象如图乙所示,t0时刻物块到达最高点,3t0时刻物块又返回底端.由此可以确定( )
如图甲所示,一物块在t=0时刻,以初速度V0从足够长的粗糙斜面底端向上滑行,物块速度随时间变化的图象如图乙所示,t0时刻物块到达最高点,3t0时刻物块又返回底端.由此可以确定( )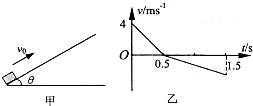 如图甲所示,一物块在t=0时刻,以初速度v0=4m/s从足够长的粗糙斜面底端向上滑行,物块速度随时间变化的图象如图乙所示,t=0.5s时刻物块到达最高点,t=1.5s时刻物块又 返回底端.求:
如图甲所示,一物块在t=0时刻,以初速度v0=4m/s从足够长的粗糙斜面底端向上滑行,物块速度随时间变化的图象如图乙所示,t=0.5s时刻物块到达最高点,t=1.5s时刻物块又 返回底端.求: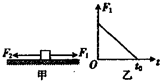
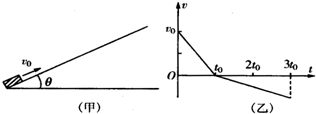 如图甲所示,一物块在t=0时刻,以初速度v0从足够长的粗糙斜面底端向上滑行,物块速度随时间变化的图象如图乙所示,t0时刻物块到达最高点,3t0时刻物块又返回底端.由此可以确定( )
如图甲所示,一物块在t=0时刻,以初速度v0从足够长的粗糙斜面底端向上滑行,物块速度随时间变化的图象如图乙所示,t0时刻物块到达最高点,3t0时刻物块又返回底端.由此可以确定( )