题目内容
【题目】如图所示，一圆管放在水平地面上，长为L=0.5m，圆管的上表面离天花板距离h=2.5m，在圆管的正上方紧靠天花板放一颗小球，让小球由静止释放，同时给圆管一竖直向上大小为5m/s的初速度，g取10m/s．
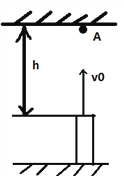
（1）求小球释放后经过多长时间与圆管相遇？
（2）试判断在圆管落地前小球能不能穿过圆管？如果不能，小球和圆管落地的时间差多大？如果能，小球穿过圆管的时间多长？
【答案】（1）0.5s（2）0.1s
【解析】试题分析：小球自由落体，圆管竖直上抛，以小球为参考系，则圆管相对小球向上以5m/s做匀速直线运动；先根据位移时间关系公式求解圆管落地的时间；再根据位移时间关系公式求解该时间内小球的位移（假设小球未落地），比较即可；再以小球为参考系，计算小球穿过圆管的时间．
（1）以小球为参考系，则圆管相对小球向上以5m/s做匀速直线运动，
故相遇时间为： 
（2）圆管做竖直上抛运动，以向上为正，根据位移时间关系公式，有
带入数据，有
，解得：t=1s 或 t=0（舍去）；
假设小球未落地，在1s内小球的位移为
，
而开始时刻小球离地的高度只有3m，故在圆管落地前小球能穿过圆管；
再以小球为参考系，则圆管相对小球向上以5m/s做匀速直线运动，
故小球穿过圆管的时间
练习册系列答案
相关题目
