题目内容
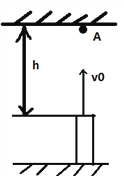
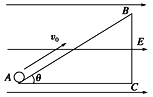
【题目】物体以一定的初速度v0冲上固定的光滑斜面，到达斜面最高点C时速度恰为零，如图所示。已知物体第一次运动到斜面长度3/4处的B点时，所用时间为t，求物体从B滑到C所用的时间。
【答案】 t
【解析】解法一 比例法
对于初速度为0的匀加速直线运动，在连续相等的时间里通过的位移之比为
x1:x2:x3:···:xn=1:3:5:···(2n–1)
现有xBC:xAB=
:
=1:3
通过xAB的时间为t，故通过xBC的时间tBC=t
解法二 中间时刻速度法
利用教材中的推论：中间时刻的瞬时速度等于这段位移的平均速度
vAC=
又v=2axAC①
v=2axBC②
xBC=③
解①②③得：
可以看出vB正好等于AC段的平均速度，因此B点是中间时刻的位置
因此有tBC=t
解法三 利用有关推论
对于初速度为0的匀加速直线运动，通过连续相等的各段位移所
用的时间之比为t1:t2:t3:···:tn=1:(
–1):(
–):···
现将整个斜面分成相等的四段，如图所示。设通过BC段的时间为tx，那么通过BD、DE、EA的时间分别为：
tBD=(–1)tx，tDE=(–)tx，tEA=(2–)tx
又tBD+tDE+tEA=t，得tx=t
名校课堂系列答案【题目】科学探究活动通常包括以下环节：提出问题，作出假设，制定计划，搜集证据，评估交流等。一组同学研究“运动物体所受空气阻力与运动速度关系”的探究过程如下：
A．有同学认为：运动物体所受空气阻力可能与其运动速度有关
B．他们计划利用一些“小纸杯”作为研究对象，用超声测距仪等仪器测量“小纸杯”在空中直线下落时的下落距离、速度随时间变化的规律，以验证假设
C．在相同的实验条件下，同学们首先测量了单只“小纸杯”在空中下落过程中不同时刻的下落距离，将数据填入表中，如图（a）是对应的位移—时间图线。然后将不同数量的“小纸杯”叠放在一起从空中下落，分别测出它们的速度—时间图线，如图（b）中图线1、2、3、4、5所示
D．同学们对实验数据进行分析、归纳后，证实了他们的假设
回答下列提问：
（1）与上述过程中A、C步骤相应的科学探究环节分别是________、________；
（2）图（a）中的AB段反映了运动物体在做________运动，表中x处的值为________；
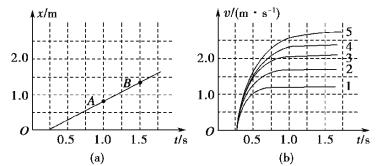（3）图（b）中各条图线具有共同特点，“小纸杯”在下落的开始阶段做__________运动，最后“小纸杯”做________运动；
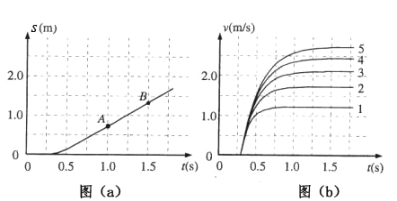
时间（s） | 下落距离（m） | 时间（s） | 下落距离（m） |
0.0 | 0.000 | 1.2 | 0.957 |
0.4 | 0.036 | 1.6 | 1.447 |
0.8 | 0.469 | 2.0 | x |
