题目内容
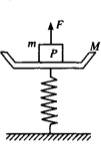
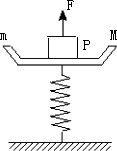
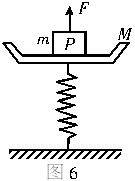
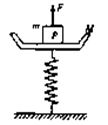
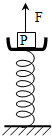一弹簧秤的秤盘质量m1=1.5kg，盘内放一质量为m2=10.5kg的物体P，弹簧质量不计，其劲度系数为K=800N/m，系统处于静止状态，如图所示．现给P施加一个竖直向上的力F，使P从静止开始向上做匀加速直线运动，已知在最初0.2s内F是变化的，在0.2s后是恒定的，求F的最大值和最小值各是多少？（g=10m/s2）分析：在P、Q分离之前，F为变力，逐渐减小；分离后，F为恒力；
两物体分离瞬间，P对Q恰好无弹力，此后Q的加速度将减小，两个物体开始分离，从开始到分离历时0.2s，由分析可知，刚开始时F最小，F为恒力时最大．
两物体分离瞬间，P对Q恰好无弹力，此后Q的加速度将减小，两个物体开始分离，从开始到分离历时0.2s，由分析可知，刚开始时F最小，F为恒力时最大．
解答：解：设刚开始时弹簧压缩量为x1，则：
x1=
=0.15m…①
设两者刚好分离时，弹簧压缩量为x2，则对Q：
kx2-m1g=m1a…②
在前0.2s时间内，由运动学公式得：
x1-x2=
at2…③
由①②③解得：a=6m/s2
由牛顿第二定律，开始时：
Fmin=（m1+m2）a=72N
最终分离后：
Fmax-m2g=m2a
即：Fmax=m2（g+a）=168N
答：力F最小为72N，最大为168N．
x1=
| (m1+m2)g |
| k |
设两者刚好分离时，弹簧压缩量为x2，则对Q：
kx2-m1g=m1a…②
在前0.2s时间内，由运动学公式得：
x1-x2=
| 1 |
| 2 |
由①②③解得：a=6m/s2
由牛顿第二定律，开始时：
Fmin=（m1+m2）a=72N
最终分离后：
Fmax-m2g=m2a
即：Fmax=m2（g+a）=168N
答：力F最小为72N，最大为168N．
点评：弹簧的弹力是变力，分析好何时两者分离是关键，此时两者间无作用力，且两者加速度刚好相等，另外牛顿定律与运动学公式的熟练应用也是同学必须掌握的
练习册系列答案
相关题目
