题目内容
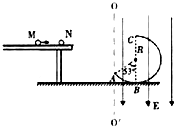
一质量为m1=1kg、带电量为q=0.5c的小球/V静止在光滑水平平台上,另一质 量为m2=1kg、不带电的小球M自平台左端以速度v=4.5m/s向右运动,两小球发生完全 弹性碰撞后,小球N自平台右端水平飞出,碰撞过程小球N的电荷量不变,不计空气阻力,小球N飞离平台后由λ点沿切线落入竖直光滑圆轨道ABC,圆轨道ABC的形状为半径R<4m的圆截去了左上角127°的圆弧,CB为其竖直直径,在过A点的竖直线00'的右边空间存 在竖直向下的匀强电场,电场强度大小为E=10V/m,(sin53°=0.8,cos53°=0.6,重力加速度g取 10m/s2)求:(1)两球碰撞后小球N的速度大小vN
(2)小球N经过A点的速度大vA
(3)欲使小球N在圆轨道运动时不脱离圆轨道,求 半径R的取值应满足什么条件?
【答案】分析:(1)两小球发生完全弹性碰撞,动量和机械能均守恒,由两大守恒定律列式,求两球碰撞后小球N的速度大小vN.
(2)小球离开平台后做平抛运动,由题知,小球经过A点时的速度沿圆轨道的切线方向,根据速度分解求出经过A点时的速度大小vA.
(3)欲使小球N在圆轨道运动时不脱离圆轨道,有两种情况:一种恰好能通过最高点C,由重力和电场力的合力提供向心力,另一种恰好滑到与圆心等高的点速度为零,根据牛顿第二定律和动能定理结合进行求解.
解答:解:(1)由题意,两小球发生完全弹性碰撞,根据动量守恒和机械能守恒,得
m2v=m1vN+m2vM
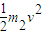 =
=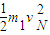 +
+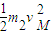
联立解得:vN=4.5m/s
(2)小球离开平台后做平抛运动,由题知,小球经过A点时的速度沿圆轨道的切线方向,则
cos53°=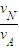
解得vA=7.5m/s
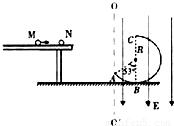
(3)(i)小球N沿切线落入竖直光滑圆轨道ABC后,小球沿轨道做圆周运动,若恰好能通过最高点C,由重力和电场力的合力提供向心力,设滑至最高点的速度为vC,则有
m1g+qE=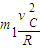
根据动能定理得:
-(m1g+qE)R(1+cos53°)=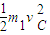 -
-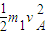
联立以上两式解得 R=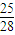 m
m
故当0<R≤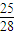 m时,小球N沿着轨道做圆周运动的,且能从圆的最高点C飞出.
m时,小球N沿着轨道做圆周运动的,且能从圆的最高点C飞出.
(ii)若小球N恰好滑到与圆心等高的圆弧上的T点时速度为零,则滑块也沿圆轨道运动而不脱离圆轨道.根据动能定理得
-(m1g+qE)Rcos53°=0-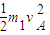
解得,R=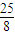 m
m
根据题中信息可知R<4m.故当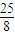 m≤R<4m时,小球在轨道内来回的滚动.
m≤R<4m时,小球在轨道内来回的滚动.
综上所术,小球能沿圆轨道运动而不脱离圆轨道,半径R的取值应满足0<R≤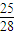 m或
m或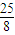 m≤R<4m.
m≤R<4m.
答:
(1)两球碰撞后小球N的速度大小vN是4.5m/s.
(2)小球N经过A点的速度大vA是7.5m/s
(3)欲使小球N在圆轨道运动时不脱离圆轨道,半径R的取值应满足0<R≤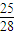 m或
m或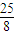 m≤R<4m.
m≤R<4m.
点评:本题是复杂的力学综合题,整合了动量守恒、机械能守恒、动能定理、向心力等等多个力学规律,特别是第3题小球能沿圆轨道运动而不脱离圆轨道,有两种可能的情况,不要漏解.
(2)小球离开平台后做平抛运动,由题知,小球经过A点时的速度沿圆轨道的切线方向,根据速度分解求出经过A点时的速度大小vA.
(3)欲使小球N在圆轨道运动时不脱离圆轨道,有两种情况:一种恰好能通过最高点C,由重力和电场力的合力提供向心力,另一种恰好滑到与圆心等高的点速度为零,根据牛顿第二定律和动能定理结合进行求解.
解答:解:(1)由题意,两小球发生完全弹性碰撞,根据动量守恒和机械能守恒,得
m2v=m1vN+m2vM
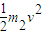 =
=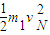 +
+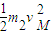
联立解得:vN=4.5m/s
(2)小球离开平台后做平抛运动,由题知,小球经过A点时的速度沿圆轨道的切线方向,则
cos53°=
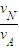
解得vA=7.5m/s
(3)(i)小球N沿切线落入竖直光滑圆轨道ABC后,小球沿轨道做圆周运动,若恰好能通过最高点C,由重力和电场力的合力提供向心力,设滑至最高点的速度为vC,则有
m1g+qE=
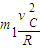
根据动能定理得:
-(m1g+qE)R(1+cos53°)=
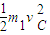 -
-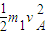
联立以上两式解得 R=
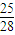 m
m故当0<R≤
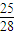 m时,小球N沿着轨道做圆周运动的,且能从圆的最高点C飞出.
m时,小球N沿着轨道做圆周运动的,且能从圆的最高点C飞出.(ii)若小球N恰好滑到与圆心等高的圆弧上的T点时速度为零,则滑块也沿圆轨道运动而不脱离圆轨道.根据动能定理得
-(m1g+qE)Rcos53°=0-
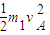
解得,R=
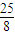 m
m根据题中信息可知R<4m.故当
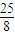 m≤R<4m时,小球在轨道内来回的滚动.
m≤R<4m时,小球在轨道内来回的滚动.综上所术,小球能沿圆轨道运动而不脱离圆轨道,半径R的取值应满足0<R≤
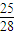 m或
m或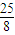 m≤R<4m.
m≤R<4m. 答:
(1)两球碰撞后小球N的速度大小vN是4.5m/s.
(2)小球N经过A点的速度大vA是7.5m/s
(3)欲使小球N在圆轨道运动时不脱离圆轨道,半径R的取值应满足0<R≤
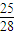 m或
m或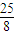 m≤R<4m.
m≤R<4m.点评:本题是复杂的力学综合题,整合了动量守恒、机械能守恒、动能定理、向心力等等多个力学规律,特别是第3题小球能沿圆轨道运动而不脱离圆轨道,有两种可能的情况,不要漏解.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
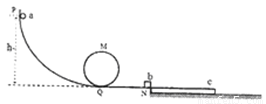
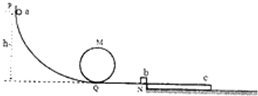 (2013?安庆二模)图中左侧部分为过山车简易模型装置,它是由弧形轨道PQ、竖直圆轨道MQ和水平轨道QN组成.所有轨道都光滑且之间均平滑对接,圆形轨道半径R=0.5m,一质量为m1=1kg的小球a从离水平轨道高为h=5m的地方沿弧形轨道静止滑下,经圆轨道运动一周后与静止在N处的小物块b发生正碰,碰后小球a沿原路返回到M点时,对轨道的压力恰好为0.碰后小物块b滑上一足够长的木板c上,已知物块b与木板c之间的动摩擦因数为μ1=0.4,木板c与地面之间的动摩擦因数μ2=0.1,物块b的质量为m2=3kg,木板c的质量为m3=4.5kg,g取10m/s2,求:
(2013?安庆二模)图中左侧部分为过山车简易模型装置,它是由弧形轨道PQ、竖直圆轨道MQ和水平轨道QN组成.所有轨道都光滑且之间均平滑对接,圆形轨道半径R=0.5m,一质量为m1=1kg的小球a从离水平轨道高为h=5m的地方沿弧形轨道静止滑下,经圆轨道运动一周后与静止在N处的小物块b发生正碰,碰后小球a沿原路返回到M点时,对轨道的压力恰好为0.碰后小物块b滑上一足够长的木板c上,已知物块b与木板c之间的动摩擦因数为μ1=0.4,木板c与地面之间的动摩擦因数μ2=0.1,物块b的质量为m2=3kg,木板c的质量为m3=4.5kg,g取10m/s2,求: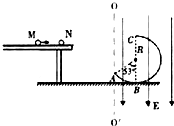 (2013?梅州一模)一质量为m1=1kg、带电量为q=0.5c的小球/V静止在光滑水平平台上,另一质 量为m2=1kg、不带电的小球M自平台左端以速度v=4.5m/s向右运动,两小球发生完全 弹性碰撞后,小球N自平台右端水平飞出,碰撞过程小球N的电荷量不变,不计空气阻力,小球N飞离平台后由λ点沿切线落入竖直光滑圆轨道ABC,圆轨道ABC的形状为半径R<4m的圆截去了左上角127°的圆弧,CB为其竖直直径,在过A点的竖直线00'的右边空间存 在竖直向下的匀强电场,电场强度大小为E=10V/m,(sin53°=0.8,cos53°=0.6,重力加速度g取 10m/s2)求:
(2013?梅州一模)一质量为m1=1kg、带电量为q=0.5c的小球/V静止在光滑水平平台上,另一质 量为m2=1kg、不带电的小球M自平台左端以速度v=4.5m/s向右运动,两小球发生完全 弹性碰撞后,小球N自平台右端水平飞出,碰撞过程小球N的电荷量不变,不计空气阻力,小球N飞离平台后由λ点沿切线落入竖直光滑圆轨道ABC,圆轨道ABC的形状为半径R<4m的圆截去了左上角127°的圆弧,CB为其竖直直径,在过A点的竖直线00'的右边空间存 在竖直向下的匀强电场,电场强度大小为E=10V/m,(sin53°=0.8,cos53°=0.6,重力加速度g取 10m/s2)求: