题目内容
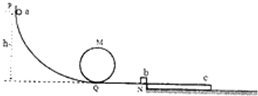 (2013?安庆二模)图中左侧部分为过山车简易模型装置,它是由弧形轨道PQ、竖直圆轨道MQ和水平轨道QN组成.所有轨道都光滑且之间均平滑对接,圆形轨道半径R=0.5m,一质量为m1=1kg的小球a从离水平轨道高为h=5m的地方沿弧形轨道静止滑下,经圆轨道运动一周后与静止在N处的小物块b发生正碰,碰后小球a沿原路返回到M点时,对轨道的压力恰好为0.碰后小物块b滑上一足够长的木板c上,已知物块b与木板c之间的动摩擦因数为μ1=0.4,木板c与地面之间的动摩擦因数μ2=0.1,物块b的质量为m2=3kg,木板c的质量为m3=4.5kg,g取10m/s2,求:
(2013?安庆二模)图中左侧部分为过山车简易模型装置,它是由弧形轨道PQ、竖直圆轨道MQ和水平轨道QN组成.所有轨道都光滑且之间均平滑对接,圆形轨道半径R=0.5m,一质量为m1=1kg的小球a从离水平轨道高为h=5m的地方沿弧形轨道静止滑下,经圆轨道运动一周后与静止在N处的小物块b发生正碰,碰后小球a沿原路返回到M点时,对轨道的压力恰好为0.碰后小物块b滑上一足够长的木板c上,已知物块b与木板c之间的动摩擦因数为μ1=0.4,木板c与地面之间的动摩擦因数μ2=0.1,物块b的质量为m2=3kg,木板c的质量为m3=4.5kg,g取10m/s2,求:(1)小球a第一次经过圆形轨道最低点时的速度;
(2)碰后瞬间小物块b的速度;
(3)木板c运动的总位移.
分析:1、球a从P点运动到圆形轨道最低点Q过程,根据机械能守恒定律求出Q的速度
2、根据牛顿第二定律求出球返回到圆轨道最高点M时的速度,球由N返回到M的过程中,根据动能定理列出等式,
再根据球a与物块b组成的系统动量守恒求解.
3、分析物块b和木板c的运动情况,根据牛顿第二定律和运动学公式求解.
2、根据牛顿第二定律求出球返回到圆轨道最高点M时的速度,球由N返回到M的过程中,根据动能定理列出等式,
再根据球a与物块b组成的系统动量守恒求解.
3、分析物块b和木板c的运动情况,根据牛顿第二定律和运动学公式求解.
解答:解:(1)设球a从P点运动到圆形轨道最低点Q时的速度大小为v,
根据机械能守恒定律:
m1gh=
m1v2
解得:v=10m/s,方向水平向右
(2)设球a与物块b碰撞后的速度大小分别为v1、v2,
球返回到圆轨道最高点M时的速度大小为v′1
根据牛顿第二定律,由向心力公式得:
m1g=m1
球由N返回到M的过程中,根据动能定理得:
-m1g?2R=
m1v′1 2-
m1v12
球a与物块b发生无机械能损失的弹性正碰,由于轨道光滑,球a碰撞前的速度与第一次到轨道最低点的速度相等,
该过程中球a与物块b组成的系统动量守恒,规定向右为正方向,
故:m1v=-m1v1+m2v2
联立解得:v2=5m/s 方向水平向右
(3)物块b滑上木板c时,设物块b和木板c的加速度大小分别a1,a2,两者经过时间达到共同的速度v3.
木块在此过程中的位移为x1,根据牛顿第二定律得:
μ1m2g=m2a1
μ1m2g-μ2(m2+m3)g=m3a2
根据运动学公式得:
v3=v2-a1t
v3=a2t
x1=
a2t2
联立解得:x1=0.5m,v3=1m/s
达共同速度后,物块b和木板c一道做匀减速直线运动直至停止,设该过程中减速的位移为x2
由动能定理得:-μ2(m2+m3)gx2=0-
(m2+m3)v32
解得:x2=0.5m
则木板c的总位移x=x1+x2=1m,方向水平向右.
答:(1)小球a第一次经过圆形轨道最低点时的速度大小是10m/s,方向水平向右;
(2)碰后瞬间小物块b的速度大小是5m/s,方向水平向右;
(3)木板c运动的总位移大小是1m,方向水平向右.
根据机械能守恒定律:
m1gh=
| 1 |
| 2 |
解得:v=10m/s,方向水平向右
(2)设球a与物块b碰撞后的速度大小分别为v1、v2,
球返回到圆轨道最高点M时的速度大小为v′1
根据牛顿第二定律,由向心力公式得:
m1g=m1
| v′1 2 |
| R |
球由N返回到M的过程中,根据动能定理得:
-m1g?2R=
| 1 |
| 2 |
| 1 |
| 2 |
球a与物块b发生无机械能损失的弹性正碰,由于轨道光滑,球a碰撞前的速度与第一次到轨道最低点的速度相等,
该过程中球a与物块b组成的系统动量守恒,规定向右为正方向,
故:m1v=-m1v1+m2v2
联立解得:v2=5m/s 方向水平向右
(3)物块b滑上木板c时,设物块b和木板c的加速度大小分别a1,a2,两者经过时间达到共同的速度v3.
木块在此过程中的位移为x1,根据牛顿第二定律得:
μ1m2g=m2a1
μ1m2g-μ2(m2+m3)g=m3a2
根据运动学公式得:
v3=v2-a1t
v3=a2t
x1=
| 1 |
| 2 |
联立解得:x1=0.5m,v3=1m/s
达共同速度后,物块b和木板c一道做匀减速直线运动直至停止,设该过程中减速的位移为x2
由动能定理得:-μ2(m2+m3)gx2=0-
| 1 |
| 2 |
解得:x2=0.5m
则木板c的总位移x=x1+x2=1m,方向水平向右.
答:(1)小球a第一次经过圆形轨道最低点时的速度大小是10m/s,方向水平向右;
(2)碰后瞬间小物块b的速度大小是5m/s,方向水平向右;
(3)木板c运动的总位移大小是1m,方向水平向右.
点评:本题涉及到三个物体,多个运动过程,属于多体多过程问题,难度较大,是一道难题;分析清楚物体运动过程是正确解题的前提与关键.

练习册系列答案
相关题目
 (2013?安庆二模)如图所示,实线为某电场的电场线,一个带电粒子(不计重力)在电场力作用下从A点沿虚线运动到B点,下列说法正确的是( )
(2013?安庆二模)如图所示,实线为某电场的电场线,一个带电粒子(不计重力)在电场力作用下从A点沿虚线运动到B点,下列说法正确的是( ) (2013?安庆二模)如图所示为一理想变压器与其它电学元件组成的电路,期中电流表、电压表均为理想电表,R为滑动变阻器,保持原线圈输入电压(有效值)不变,当滑片向上移动过程中,下列说法正确的是( )
(2013?安庆二模)如图所示为一理想变压器与其它电学元件组成的电路,期中电流表、电压表均为理想电表,R为滑动变阻器,保持原线圈输入电压(有效值)不变,当滑片向上移动过程中,下列说法正确的是( ) (2013?安庆二模)2013年2月15日中午12时30分左右,俄罗斯车里雅宾斯克州发生天体坠落事件.根据俄紧急情况部的说法,坠落的是一颗陨石.这颗陨石重量接近1万吨,进入地球大气层的速度约为4万英里每小时,随后与空气摩擦而发生剧烈燃烧,并在距离地面上空12至15英里处发生爆炸,产生大量碎片,假定某一碎片自爆炸后落至地面并陷入地下一定深度过程中,其质量不变,则( )
(2013?安庆二模)2013年2月15日中午12时30分左右,俄罗斯车里雅宾斯克州发生天体坠落事件.根据俄紧急情况部的说法,坠落的是一颗陨石.这颗陨石重量接近1万吨,进入地球大气层的速度约为4万英里每小时,随后与空气摩擦而发生剧烈燃烧,并在距离地面上空12至15英里处发生爆炸,产生大量碎片,假定某一碎片自爆炸后落至地面并陷入地下一定深度过程中,其质量不变,则( )