题目内容
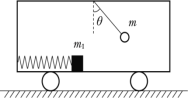
【题目】在水平地面上运动的小车车厢底部有一质量为m1的木块,木块和车厢通过一根水平轻弹簧相连接,弹簧的劲度系数为k,在车厢的顶部用一根细线悬挂一质量为m的小球。某段时间内发现细线与竖直方向的夹角为θ,在这段时间内木块与车厢保持相对静止,弹簧的形变量为x,如图所示。不计木块与车厢底部的摩擦力,则在这段时间内( )
A. 小车一定向左做加速运动
B. 弹簧可能处于压缩状态
C. 小车的加速度方向向左,大小为![]()
D. 弹簧的形变量为![]()
【答案】D
【解析】
小球、木块和小车具有相同的加速度,隔离对小球分析,根据牛顿第二定律求出小球的加速度,对m1受力分析,由牛顿第二定律求弹簧的形变量。
由题意知,木块、小车、小球相对静止,具有相同的加速度,对小球进行受力分析有:小球受重力和细线的拉力,在两个力作用下小球在竖直方向处于平衡状态,水平方向产生加速度,所以有:Tsinθ=ma,Tcosθ=mg;所以可得小球的加速度a=gtanθ,方向水平向左,则小车的加速度为a=gtanθ,方向水平向左,而小车的速度方向不确定,所以小车可能向左做加速运动,也可能向右减速运动,故AC错误。对m1分析知,m1的加速度水平向左,合力水平向左,弹簧对m1必定有水平向左的拉力,所以弹簧一定处于伸长状态,故B错误。对m1,由牛顿第二定律,得:kx=m1a,解得x=![]() tanθ,故D正确,故选D。
tanθ,故D正确,故选D。

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目