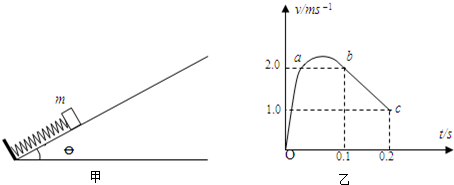题目内容
2.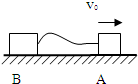 光滑水平面上用细线相连的A、B两物体,它们的质量分别为m1和m2,A以v0的速度向右滑动,如图所示,当细线拉直后,A、B一起运动的速度为$\frac{{m}_{1}{v}_{0}}{{m}_{1}+{m}_{2}}$,绳子张力对A的冲量大小为$\frac{{m}_{1}{{m}_{2}v}_{0}}{{m}_{1}+{m}_{2}}$.
光滑水平面上用细线相连的A、B两物体,它们的质量分别为m1和m2,A以v0的速度向右滑动,如图所示,当细线拉直后,A、B一起运动的速度为$\frac{{m}_{1}{v}_{0}}{{m}_{1}+{m}_{2}}$,绳子张力对A的冲量大小为$\frac{{m}_{1}{{m}_{2}v}_{0}}{{m}_{1}+{m}_{2}}$.
分析 (1)由动量守恒定律可以求出A、B的共同速度;
(2)由动量定理可以求出冲量;
解答 解:A、B组成的系统动量守恒,以A的初速度方向为正方向,由动量守恒定律得:
m1v0=(m1+m2)v,
解得:v=$\frac{{m}_{1}{v}_{0}}{{m}_{1}+{m}_{2}}$;
对A,由动量定理得:I=m1v-m1v0,
解得:I=-$\frac{{m}_{1}{{m}_{2}v}_{0}}{{m}_{1}+{m}_{2}}$,负号表示方向,即绳子张力对A的冲量大小为$\frac{{m}_{1}{{m}_{2}v}_{0}}{{m}_{1}+{m}_{2}}$.
故答案为:$\frac{{m}_{1}{v}_{0}}{{m}_{1}+{m}_{2}}$;$\frac{{m}_{1}{{m}_{2}v}_{0}}{{m}_{1}+{m}_{2}}$
点评 本题考查了求速度、冲量等问题,应用动量守恒定律、动量定理定律即可正确解题,难度不大,属于基础题.

练习册系列答案
相关题目
17.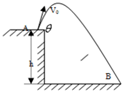 把质量m的小球从距离地面高为h处以θ角斜向上方抛出,初速度为v0.不计空气阻力,小球落地时的速度大小与下列因素有关的是( )
把质量m的小球从距离地面高为h处以θ角斜向上方抛出,初速度为v0.不计空气阻力,小球落地时的速度大小与下列因素有关的是( )
 把质量m的小球从距离地面高为h处以θ角斜向上方抛出,初速度为v0.不计空气阻力,小球落地时的速度大小与下列因素有关的是( )
把质量m的小球从距离地面高为h处以θ角斜向上方抛出,初速度为v0.不计空气阻力,小球落地时的速度大小与下列因素有关的是( )| A. | 小球的初速度v0的大小 | B. | 小球的质量m | ||
| C. | 零势面的选取 | D. | 小球抛出时的仰角θ |
7.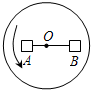 如图,在匀速转动的水平圆盘上,沿直径方向放着用细线相连的质量相等的两个物体A和B,它们与盘面间的动摩擦因数相同.A到圆盘中心的距离是B到圆盘中心距离的一半,当匀速转动的圆盘转速恰为两物体刚好未发生滑动时的转速,烧断细线,则两个物体的运动情况将是( )
如图,在匀速转动的水平圆盘上,沿直径方向放着用细线相连的质量相等的两个物体A和B,它们与盘面间的动摩擦因数相同.A到圆盘中心的距离是B到圆盘中心距离的一半,当匀速转动的圆盘转速恰为两物体刚好未发生滑动时的转速,烧断细线,则两个物体的运动情况将是( )
 如图,在匀速转动的水平圆盘上,沿直径方向放着用细线相连的质量相等的两个物体A和B,它们与盘面间的动摩擦因数相同.A到圆盘中心的距离是B到圆盘中心距离的一半,当匀速转动的圆盘转速恰为两物体刚好未发生滑动时的转速,烧断细线,则两个物体的运动情况将是( )
如图,在匀速转动的水平圆盘上,沿直径方向放着用细线相连的质量相等的两个物体A和B,它们与盘面间的动摩擦因数相同.A到圆盘中心的距离是B到圆盘中心距离的一半,当匀速转动的圆盘转速恰为两物体刚好未发生滑动时的转速,烧断细线,则两个物体的运动情况将是( )| A. | 细线烧断前一定有张力 | |
| B. | 烧断细线后,两物体均沿半径方向滑动,离圆盘圆心越来越远 | |
| C. | 烧断细线后,两物体受到圆盘的摩擦力大小相等 | |
| D. | 烧断细线后,物体A仍随圆盘一起做匀速圆周运动,物体B发生滑动 |
12.下列说法中正确的是( )
| A. | 做曲线运动的物体一定是具有加速度 | |
| B. | 做曲线运动的物体所受的合外力可以为零 | |
| C. | 做曲线运动的物体的速度可以不变化 | |
| D. | 做曲线运动的物体所受合力一定与速度垂直 |
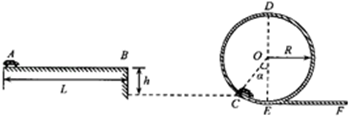
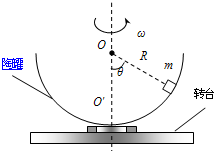 如图所示,半径为R的半球形陶罐,固定在可以绕竖直轴旋转的水平转台上,转台转轴与过陶罐球心O的对称轴OO′重合.转台以一定角速度ω匀速转动,一质量为m的小物块落入陶罐内,经过一段时间后小物块随陶罐一起转动且相对罐壁静止,它和O点的连线与OO′之间的夹角θ为60°,重力加速度大小为g.
如图所示,半径为R的半球形陶罐,固定在可以绕竖直轴旋转的水平转台上,转台转轴与过陶罐球心O的对称轴OO′重合.转台以一定角速度ω匀速转动,一质量为m的小物块落入陶罐内,经过一段时间后小物块随陶罐一起转动且相对罐壁静止,它和O点的连线与OO′之间的夹角θ为60°,重力加速度大小为g.