题目内容
20. 将质量为m的物体在高空中以速率υ水平向右抛出,由于风力作用,经过时间t后,物体下落一段高度,速率仍为υ,方向与初速度相反,如图所示.在这一运动过程中,下列关于风力做功的说法,正确的是( )
将质量为m的物体在高空中以速率υ水平向右抛出,由于风力作用,经过时间t后,物体下落一段高度,速率仍为υ,方向与初速度相反,如图所示.在这一运动过程中,下列关于风力做功的说法,正确的是( )| A. | 风力对物体不做功 | |
| B. | 风力对物体做的功(绝对值)为$\frac{{m{g^2}{t^2}}}{2}$ | |
| C. | 风力对物体做的功(绝对值)小于$\frac{{m{g^2}{t^2}}}{2}$ | |
| D. | 由于风力方向未知,不能判断风力做功情况 |
分析 结合运动的分解判断风力的方向,运用动能定理判断风力做功情况.
解答 解:ABC、对物体A运用动能定理得:WG+W风=$\frac{1}{2}$mv2-$\frac{1}{2}$mv2=0.由于重力做正功,所以风力做负功;
水平方向上,物体先向右减速后向左加速,故一定有向左的风力;
竖直方向上,物体先加速后减速,说明风力先小于重力,后大于重力,有向上的风力,所以竖直方向的分位移小于自由落体运动的位移$\frac{1}{2}g{t}^{2}$,则重力做功 WG<mg•$\frac{1}{2}g{t}^{2}$=$\frac{{m{g^2}{t^2}}}{2}$,故ABD错误,C正确;
故选:C
点评 本题关键将物体的运动沿着水平和竖直方向正交分解,然后结合牛顿运动定律分析物体的受力情况.要知道动能定理是研究做功情况常用的方法.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
19.关于摩擦力,有人总结了“四条不一定”,其中说法错误的是( )
| A. | 受静摩擦力或滑动摩擦力的物体不一定静止或运动 | |
| B. | 摩擦力不一定是阻力 | |
| C. | 滑动摩擦力不一定阻碍物体间的相对运动 | |
| D. | 摩擦力的方向不一定与物体的运动方向相同 |
15.在用DIS实验研究小车加速度与外力的关系时,某实验小组先用如图(a)所示的实验装置,重物通过滑轮用细线拉小车,位移传感器(发射器)随小车一起沿倾斜轨道运动,位移传感器(接收器)固定在轨道一端.实验中把重物的重力作为拉力F,改变重物重力重复实验四次,列表记录四组数据.
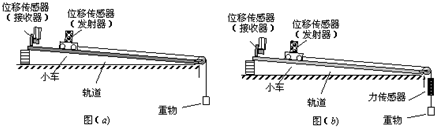
(1)在图(c)坐标纸上作出小车加速度a和拉力F的关系图线;
(2)从所得图线分析该实验小组在操作过程中的不当之处是倾角过大或平衡摩擦力过度;
(3)如果实验时,在小车和重物之间接一个不计质量的微型力传感器来测量绳子的拉力大小,如图(b)所示.要满足小车质量M远大于重物的质量m是不必要的.(填“必要”或“不必要”)
(4)如果实验装置如图(a),图为质量一定时,根据实验数据描绘的小车加速度a与重物的总质量m之间的关系图象.设图(d)中直线斜率为k,在纵轴上的斜率为b,若牛顿第二定律成立,则小车的重量G为$\frac{k}{{b}^{2}}$;当地的重力加速度为$\frac{1}{b}$.
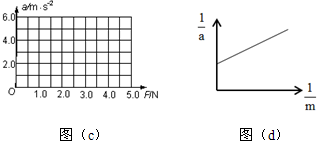

(1)在图(c)坐标纸上作出小车加速度a和拉力F的关系图线;
(2)从所得图线分析该实验小组在操作过程中的不当之处是倾角过大或平衡摩擦力过度;
(3)如果实验时,在小车和重物之间接一个不计质量的微型力传感器来测量绳子的拉力大小,如图(b)所示.要满足小车质量M远大于重物的质量m是不必要的.(填“必要”或“不必要”)
| a/ms-2 | 2.01 | 2.98 | 4.02 | 6.00 |
| F/N | 1.00 | 2.00 | 3.00 | 5.00 |

5. 如图所示,一平行板电容器的两极板与一电压恒定的电源相连,极板水平放置,极板间距为d,有一带电粒子P静止在电容器上部空间中,当在其下极板上快速插入一厚度为l的不带电的金属板后,粒子P开始运动,重力加速度为g.粒子运动加速度大小为( )
如图所示,一平行板电容器的两极板与一电压恒定的电源相连,极板水平放置,极板间距为d,有一带电粒子P静止在电容器上部空间中,当在其下极板上快速插入一厚度为l的不带电的金属板后,粒子P开始运动,重力加速度为g.粒子运动加速度大小为( )
 如图所示,一平行板电容器的两极板与一电压恒定的电源相连,极板水平放置,极板间距为d,有一带电粒子P静止在电容器上部空间中,当在其下极板上快速插入一厚度为l的不带电的金属板后,粒子P开始运动,重力加速度为g.粒子运动加速度大小为( )
如图所示,一平行板电容器的两极板与一电压恒定的电源相连,极板水平放置,极板间距为d,有一带电粒子P静止在电容器上部空间中,当在其下极板上快速插入一厚度为l的不带电的金属板后,粒子P开始运动,重力加速度为g.粒子运动加速度大小为( )| A. | $\frac{l}{d}$g | B. | $\frac{d-l}{d}$g | C. | $\frac{l}{d-l}$g | D. | $\frac{d}{d-l}$g |
10.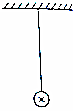 有一根质量为m、长度为d的通有水平向里的电流I的导体棒,被长度为L的轻质绝缘细线悬挂在天花板上,在此空间加上竖直向下的匀强磁场,磁场的磁感应强度大小为B=$\frac{\sqrt{3}mg}{3Id}$,若保持导体棒中的电流I始终不变,则( )
有一根质量为m、长度为d的通有水平向里的电流I的导体棒,被长度为L的轻质绝缘细线悬挂在天花板上,在此空间加上竖直向下的匀强磁场,磁场的磁感应强度大小为B=$\frac{\sqrt{3}mg}{3Id}$,若保持导体棒中的电流I始终不变,则( )
 有一根质量为m、长度为d的通有水平向里的电流I的导体棒,被长度为L的轻质绝缘细线悬挂在天花板上,在此空间加上竖直向下的匀强磁场,磁场的磁感应强度大小为B=$\frac{\sqrt{3}mg}{3Id}$,若保持导体棒中的电流I始终不变,则( )
有一根质量为m、长度为d的通有水平向里的电流I的导体棒,被长度为L的轻质绝缘细线悬挂在天花板上,在此空间加上竖直向下的匀强磁场,磁场的磁感应强度大小为B=$\frac{\sqrt{3}mg}{3Id}$,若保持导体棒中的电流I始终不变,则( )| A. | 细线偏离竖直方向的夹角最大为30° | |
| B. | 细线偏离竖直方向的夹角最大为60° | |
| C. | 在导体棒摆动过程中细线上拉力最大为2($\sqrt{3}$-1)mg | |
| D. | 在导体棒摆动过程中细线上拉力最大为$\frac{(12+\sqrt{3})mg}{6}$ |
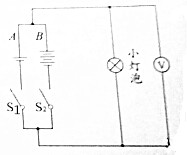 在如图中,A组电源为4节干电池,B组电源为3节蓄电池,两组的电动势均为6V.将它们与6V小灯泡、电压表、开关按图示电路连接.分别闭合开关S1和S2,将观察到小灯泡亮度和电压表示数都不同.在闭合电路中电动势和用电器都相同的情况下,用电器两端电压不相同说明了什么?
在如图中,A组电源为4节干电池,B组电源为3节蓄电池,两组的电动势均为6V.将它们与6V小灯泡、电压表、开关按图示电路连接.分别闭合开关S1和S2,将观察到小灯泡亮度和电压表示数都不同.在闭合电路中电动势和用电器都相同的情况下,用电器两端电压不相同说明了什么?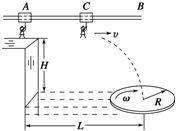 湖南卫视推出了大型户外竞技类节目《快乐向前冲》,是体力与耐力展现的一个体能竞赛活动.节目的场地设施如图所示,AB为水平直轨道,上面安装有电动悬挂器,可以载人运动,水面上漂浮着一个半径为R、角速度为ω、铺有海绵垫的转盘,转盘的轴心离平台的水平距离为L,平台边缘与转盘平面的高度差为H.选手抓住悬挂器可以在电动机的带动下,从A点下方的平台边缘处沿水平方向做初速度为零、加速度为a的匀加速直线运动.选手必须作好判断,在合适的位置释放,才能顺利落在转盘上.设人的质量为m(不计身高),人与转盘间的最大静摩擦力为μmg,重力加速度为g.
湖南卫视推出了大型户外竞技类节目《快乐向前冲》,是体力与耐力展现的一个体能竞赛活动.节目的场地设施如图所示,AB为水平直轨道,上面安装有电动悬挂器,可以载人运动,水面上漂浮着一个半径为R、角速度为ω、铺有海绵垫的转盘,转盘的轴心离平台的水平距离为L,平台边缘与转盘平面的高度差为H.选手抓住悬挂器可以在电动机的带动下,从A点下方的平台边缘处沿水平方向做初速度为零、加速度为a的匀加速直线运动.选手必须作好判断,在合适的位置释放,才能顺利落在转盘上.设人的质量为m(不计身高),人与转盘间的最大静摩擦力为μmg,重力加速度为g.