题目内容
12.在粗糙的绝缘水平面上相距为6L的A、B两处,分别固定电量不等的正点电荷,两电荷的位置坐标如图(甲)所示,其中B处电荷的电量为Q.图(乙)是AB连线之间的电势φ与位置x之间关系的图象:图中x=L点为图线的最低点,x=-2L处的纵坐标φ=φ0,x=0处的纵坐标φ=$\frac{25}{63}$φ0.x=2L处的纵坐标φ=$\frac{3}{7}$φ0,在x=-2L的C点由静止释放一个质量为m、电量为q的带正电物块(可视为质点),物块随即向右运动.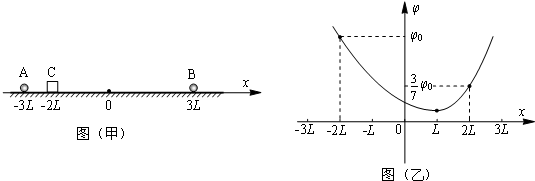
求:
(1)固定在A处的电荷的电量QA;
(2)小物块与水平面间的动摩擦因数μ应多大,才能使小物块恰好到达x=2L处;
(3)若小物块与水平面间的动摩擦因数μ=$\frac{kqQ}{3mg{L}^{2}}$,小物块运动到何处时速度最大?并求最大速度vm.
分析 (1)由图(乙)得,x=L点为图线的最低点,切线斜率为零,即合场强E合=0,根据点电荷场强公式列方程化简,可得A处的电荷的电量.
(2)物块先做加速运动再做减速运动,到达x=2L处速度vt≥0,从x=-2L到x=2L过程中,由动能定理列式,可解得动摩擦因数.
(3)小物块运动速度最大时,电场力与摩擦力的合力为零,列平衡方程,化简解出速度最大位置距离A点的距离lA. 小物块从x=-2L运动到x=0的过程中,由动能定理解得最大速度.
解答 解:(1)由图(乙)得,x=L点为图线的最低点,切线斜率为零,即合场强E合=0
所以 k$\frac{{Q}_{A}}{{r}_{A}^{2}}$=k$\frac{{Q}_{B}}{{r}_{B}^{2}}$
代入得 k$\frac{{Q}_{A}}{(4L)^{2}}$=k$\frac{{Q}_{B}}{(2L)^{2}}$
解得QA=4QB=4Q;
(2)物块先做加速运动再做减速运动,到达x=2L处速度vt≥0
从x=-2L到x=2L过程中,由动能定理得:
qU1-μmgs1=$\frac{1}{2}$mv12-0,
即q(φ0-$\frac{3}{7}$φ0)-μmg(4L)=$\frac{1}{2}$mv12-0
解得μ=$\frac{q{φ}_{0}}{7mgL}$;
(3)小物块运动速度最大时,电场力与摩擦力的合力为零,设该位置离A点的距离为lA
则:$\frac{kq•4Q}{{l}_{A}^{2}}$-$\frac{k•qQ}{(6L-{l}_{A})^{2}}$-μmg=0
解得lA=3L,即小物块运动到x=0时速度最大.
小物块从x=-2L运动到x=0的过程中,由动能定理得:
qU2-μmgs2=$\frac{1}{2}$mvm2-0
代入数据:q(φ0-$\frac{25}{63}$φ0)-μmg(2L)=$\frac{1}{2}$mvm2-0
解得 vm=$\sqrt{\frac{76q{φ}_{0}}{63m}-\frac{4kqQ}{3mL}}$
答:
(1)固定在A处的电荷的电量QA是4Q
(2)小物块与水平面间的动摩擦因数μ应$\frac{q{φ}_{0}}{7mgL}$,才能使小物块恰好到达x=2L处;
(3)若小物块与水平面间的动摩擦因数μ=$\frac{kqQ}{3mg{L}^{2}}$,小物块运动到离A点的距离3L处时速度最大,最大速度vm是$\sqrt{\frac{76q{φ}_{0}}{63m}-\frac{4kqQ}{3mL}}$.
点评 在电场问题中运用动能定理时要注意电场力做功和路径无关,只和初末两点的电势差有关,掌握电场力做功的公式WAB=qUAB,注意各量都要代入符号.

 互动课堂系列答案
互动课堂系列答案 如图所示,质量为M的木板C放在水平地面上,固定在C上的竖直轻杆的顶端分别用细绳a和b连接小球A和小球B,小球A、B的质量分别为mA和mB,当与水平方向成30°角的力F作用在小球B上时,A、B、C刚好相对静止一起向右匀速运动,且此时绳a、b与竖直方向的夹角分别为30°和60°,则下列判断正确的是( )
如图所示,质量为M的木板C放在水平地面上,固定在C上的竖直轻杆的顶端分别用细绳a和b连接小球A和小球B,小球A、B的质量分别为mA和mB,当与水平方向成30°角的力F作用在小球B上时,A、B、C刚好相对静止一起向右匀速运动,且此时绳a、b与竖直方向的夹角分别为30°和60°,则下列判断正确的是( )| A. | mA=mB | B. | 力F的大小为 $\frac{1}{2}{m_B}g$ | ||
| C. | 地面对C的摩擦力大小为$\frac{{\sqrt{3}}}{2}{m_B}$g | D. | 地面对C的支持力等于(M+mA+mB)g |
 将质量为m的物体在高空中以速率υ水平向右抛出,由于风力作用,经过时间t后,物体下落一段高度,速率仍为υ,方向与初速度相反,如图所示.在这一运动过程中,下列关于风力做功的说法,正确的是( )
将质量为m的物体在高空中以速率υ水平向右抛出,由于风力作用,经过时间t后,物体下落一段高度,速率仍为υ,方向与初速度相反,如图所示.在这一运动过程中,下列关于风力做功的说法,正确的是( )| A. | 风力对物体不做功 | |
| B. | 风力对物体做的功(绝对值)为$\frac{{m{g^2}{t^2}}}{2}$ | |
| C. | 风力对物体做的功(绝对值)小于$\frac{{m{g^2}{t^2}}}{2}$ | |
| D. | 由于风力方向未知,不能判断风力做功情况 |
 云台山是全球首批世界地质公园,青龙峡景点有“中原第一峡谷”美誉,这里气候独特,植被原始完整,是生态旅游的好去处,乘坐索道缆车观赏怡人的风景以外,还能感觉悬挂在高空的刺激感.对于正在乘坐索道缆车观光的某游客来说,以下说法正确的是( )
云台山是全球首批世界地质公园,青龙峡景点有“中原第一峡谷”美誉,这里气候独特,植被原始完整,是生态旅游的好去处,乘坐索道缆车观赏怡人的风景以外,还能感觉悬挂在高空的刺激感.对于正在乘坐索道缆车观光的某游客来说,以下说法正确的是( )| A. | 以自己为参考系,看到同一缆车里的人向对面的山不断靠近 | |
| B. | 以对面的山为参考系,自己静止不动 | |
| C. | 以所乘坐的缆车为参考系,看到两边的绿树在向前运动 | |
| D. | 以自己为参考系,看到对面的山迎面而来 |
| A. | $\frac{4}{5}$F | B. | $\frac{5}{4}$F | C. | $\frac{16}{5}$F | D. | $\frac{12}{5}$F |
| A. | 在该行星和地球上发射卫星的第一宇宙速度相同 | |
| B. | 如果人到了该行星,其体重是地球上的$\frac{8}{3}$倍 | |
| C. | 该行星的公转半径与日地距离相等 | |
| D. | 该行星公转速率是地球的$\frac{1}{13}$ |
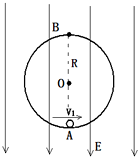 如图所示,内表面光滑绝缘的半径为1.2m的圆形轨道处于竖直平面内,有竖直向下的匀强电场,场强大小为3×106V/m.有一质量为0.12kg、带负电的小球,电荷量大小为1.6×10-6C,小球在圆轨道内壁做圆周运动,当运动到最低点A时,小球与轨道压力恰好为零,g取10m/s2,求:
如图所示,内表面光滑绝缘的半径为1.2m的圆形轨道处于竖直平面内,有竖直向下的匀强电场,场强大小为3×106V/m.有一质量为0.12kg、带负电的小球,电荷量大小为1.6×10-6C,小球在圆轨道内壁做圆周运动,当运动到最低点A时,小球与轨道压力恰好为零,g取10m/s2,求: 某同学用螺旋测微器测量一条金属丝的直径时,螺旋测微器的读数如图所示.可知该金属丝的直径d=0.900mm.
某同学用螺旋测微器测量一条金属丝的直径时,螺旋测微器的读数如图所示.可知该金属丝的直径d=0.900mm.