题目内容
8.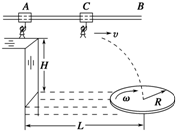 湖南卫视推出了大型户外竞技类节目《快乐向前冲》,是体力与耐力展现的一个体能竞赛活动.节目的场地设施如图所示,AB为水平直轨道,上面安装有电动悬挂器,可以载人运动,水面上漂浮着一个半径为R、角速度为ω、铺有海绵垫的转盘,转盘的轴心离平台的水平距离为L,平台边缘与转盘平面的高度差为H.选手抓住悬挂器可以在电动机的带动下,从A点下方的平台边缘处沿水平方向做初速度为零、加速度为a的匀加速直线运动.选手必须作好判断,在合适的位置释放,才能顺利落在转盘上.设人的质量为m(不计身高),人与转盘间的最大静摩擦力为μmg,重力加速度为g.
湖南卫视推出了大型户外竞技类节目《快乐向前冲》,是体力与耐力展现的一个体能竞赛活动.节目的场地设施如图所示,AB为水平直轨道,上面安装有电动悬挂器,可以载人运动,水面上漂浮着一个半径为R、角速度为ω、铺有海绵垫的转盘,转盘的轴心离平台的水平距离为L,平台边缘与转盘平面的高度差为H.选手抓住悬挂器可以在电动机的带动下,从A点下方的平台边缘处沿水平方向做初速度为零、加速度为a的匀加速直线运动.选手必须作好判断,在合适的位置释放,才能顺利落在转盘上.设人的质量为m(不计身高),人与转盘间的最大静摩擦力为μmg,重力加速度为g.(1)假设选手落到转盘上瞬间相对转盘速度立即变为零,为保证他落在任何位置都不会被甩下转盘,转盘的角速度ω应限制在什么范围?
(2)若已知H=5m,L=8m,a=2m/s2,g=10m/s2,且选手从某处C点释放能恰好落到转盘的圆心上,则他是从平台出发后多长时间释放悬挂器的?
(3)若电动悬挂器开动后,针对不同选手的动力与该选手重力关系皆为F=0.6mg,悬挂器在轨道上运动时存在恒定的摩擦阻力,选手在运动到上面(2)中所述位置C点时,因恐惧没有释放悬挂器,但立即关闭了它的电动机,则按照(2)中数据计算悬挂器载着选手还能继续向右滑行多远的距离?
分析 (1)根据静摩擦力提供向心力,结合牛顿第二定律求出转盘角速度的范围.
(2)抓住平抛运动的水平位移和匀加速直线运动的位移等于L,结合位移公式和速度公式求出匀加速运动的时间;根据平抛运动的分位移公式列式求解平抛运动的时间,即可得到总时间.
(3)对加速和减速两个过程,分别运用动能定理列式,联立可求得滑行距离.
解答 解:(1)设选手落在转盘边缘也不会被甩下,最大静摩擦力提供向心力,则有
μmg≥mω2R,故转盘转动的角速度应满足ω≤$\sqrt{\frac{μg}{R}}$
(2)设选手水平加速阶段的位移为x1,时间为t1;选手平抛时的水平位移为x2,时间为t2.则水平加速时有
x1=$\frac{1}{2}$at12;
v=at1
平抛运动阶段,有 x2=vt2,H=$\frac{1}{2}$gt22;
全程水平方向有 x1+x2=L,
联立以上各式代入数据解得 t1=2 s.
(3)由(2)知x1=4 m,v=4 m/s,且F=0.6mg.设阻力为f,选手继续向右滑动的距离为x3,由动能定理得
加速阶段有:Fx-fx=$\frac{1}{2}$mv2
减速阶段有:-fx3=0-$\frac{1}{2}$mv2
联立以上两式解得 x3=2 m.
答:
(1)转盘的角速度ω应限制在ω≤$\sqrt{\frac{μg}{R}}$范围.
(2)他是从平台出发后2s时间释放悬挂器的.
(3)悬挂器载着选手还能继续向右滑行2m的距离.
点评 解决本题的关键理清选手的运动过程,找出每个过程的物理规律,结合牛顿第二定律、平抛运动的分位移公式、运动学公式灵活解答.

练习册系列答案
相关题目
7. 如图所示,一个闭合电路内有四只不同规格的小灯泡(可认为电阻不变).原来四只灯泡的亮度相同,当滑动变阻器的滑片P向左滑动时( )
如图所示,一个闭合电路内有四只不同规格的小灯泡(可认为电阻不变).原来四只灯泡的亮度相同,当滑动变阻器的滑片P向左滑动时( )
 如图所示,一个闭合电路内有四只不同规格的小灯泡(可认为电阻不变).原来四只灯泡的亮度相同,当滑动变阻器的滑片P向左滑动时( )
如图所示,一个闭合电路内有四只不同规格的小灯泡(可认为电阻不变).原来四只灯泡的亮度相同,当滑动变阻器的滑片P向左滑动时( )| A. | D1变亮 | B. | D2变亮 | C. | D3 变亮 | D. | D4变亮 |
8. 我国游泳运动员宁泽涛在2014年仁川亚运会上一鸣惊人,获得四块金牌,其中50米自由泳金牌的角逐让人印象深刻.若宁泽涛入水后2s内通过的距离为2.388m(视为初速度为0的匀加速过程),此时达到最大速度,且保持最大速度运动的持续时间不超过20s,之后做匀减速运动,匀减速运动加速度大小为1m/s2.则宁泽涛50米的夺金成绩是( )
我国游泳运动员宁泽涛在2014年仁川亚运会上一鸣惊人,获得四块金牌,其中50米自由泳金牌的角逐让人印象深刻.若宁泽涛入水后2s内通过的距离为2.388m(视为初速度为0的匀加速过程),此时达到最大速度,且保持最大速度运动的持续时间不超过20s,之后做匀减速运动,匀减速运动加速度大小为1m/s2.则宁泽涛50米的夺金成绩是( )
 我国游泳运动员宁泽涛在2014年仁川亚运会上一鸣惊人,获得四块金牌,其中50米自由泳金牌的角逐让人印象深刻.若宁泽涛入水后2s内通过的距离为2.388m(视为初速度为0的匀加速过程),此时达到最大速度,且保持最大速度运动的持续时间不超过20s,之后做匀减速运动,匀减速运动加速度大小为1m/s2.则宁泽涛50米的夺金成绩是( )
我国游泳运动员宁泽涛在2014年仁川亚运会上一鸣惊人,获得四块金牌,其中50米自由泳金牌的角逐让人印象深刻.若宁泽涛入水后2s内通过的距离为2.388m(视为初速度为0的匀加速过程),此时达到最大速度,且保持最大速度运动的持续时间不超过20s,之后做匀减速运动,匀减速运动加速度大小为1m/s2.则宁泽涛50米的夺金成绩是( )| A. | 19.94s | B. | 21.94s | C. | 20.94s | D. | 22.94s |
13.为了“探究加速度与力、质量的关系”,现提供如图1所示实验装置.请思考探究思路并回答下列问题:

(1)为了消除小车与水平木板之间摩擦力的影响应采 取做法是C
A.将不带滑轮的木板一端垫高适当,使小车在钩码拉动下恰好做匀速运动
B.将不带滑轮的木板一端适当垫高,使小车在钩码拉动下恰好做匀加速运动
C.将不带滑轮的木板一端适当垫高,在不挂钩码的情况下使小车恰好做匀速运动
D.将不带滑轮的木板一端适当垫高,在不挂钩码的情况下使小车恰好做匀加速运动
(2)在“探究加速度与力、质量关系”的实验中,得到一条打点的纸带,如图2所示,已知相邻计数点间的时间间隔为T,且间距x1、x2、x3、x4、x5、x6已量出,则小车加速度的表达式为a=$\frac{{x}_{6}+{x}_{5}+{x}_{4}-{x}_{3}-{x}_{2}-{x}_{1}}{9{T}^{2}}$;
(3)消除小车与水平木板之间摩擦力的影响后,可用钩码总重力代替小车所受的拉力,此时钩码m与小车总质量M之间应满足的关系为m<<M;
(4)在“探究加速度与质量的关系”时,保持砝码质量不变,改变小车质量m,得到的实验数据如下表:
为了验证猜想,请在图3坐标系中作出最能直观反映a与m之间关系的图象.

(1)为了消除小车与水平木板之间摩擦力的影响应采 取做法是C
A.将不带滑轮的木板一端垫高适当,使小车在钩码拉动下恰好做匀速运动
B.将不带滑轮的木板一端适当垫高,使小车在钩码拉动下恰好做匀加速运动
C.将不带滑轮的木板一端适当垫高,在不挂钩码的情况下使小车恰好做匀速运动
D.将不带滑轮的木板一端适当垫高,在不挂钩码的情况下使小车恰好做匀加速运动
(2)在“探究加速度与力、质量关系”的实验中,得到一条打点的纸带,如图2所示,已知相邻计数点间的时间间隔为T,且间距x1、x2、x3、x4、x5、x6已量出,则小车加速度的表达式为a=$\frac{{x}_{6}+{x}_{5}+{x}_{4}-{x}_{3}-{x}_{2}-{x}_{1}}{9{T}^{2}}$;
(3)消除小车与水平木板之间摩擦力的影响后,可用钩码总重力代替小车所受的拉力,此时钩码m与小车总质量M之间应满足的关系为m<<M;
(4)在“探究加速度与质量的关系”时,保持砝码质量不变,改变小车质量m,得到的实验数据如下表:
| 实验次数 | 1 | 2 | 3 | 4 | 5 |
| 小车加速度a/ms-2 | 0.77 | 0.38 | 0.25 | 0.19 | 0.16 |
| 小车质量m/kg | 0.20 | 0.40 | 0.60 | 0.80 | 1.00 |
20. 将质量为m的物体在高空中以速率υ水平向右抛出,由于风力作用,经过时间t后,物体下落一段高度,速率仍为υ,方向与初速度相反,如图所示.在这一运动过程中,下列关于风力做功的说法,正确的是( )
将质量为m的物体在高空中以速率υ水平向右抛出,由于风力作用,经过时间t后,物体下落一段高度,速率仍为υ,方向与初速度相反,如图所示.在这一运动过程中,下列关于风力做功的说法,正确的是( )
 将质量为m的物体在高空中以速率υ水平向右抛出,由于风力作用,经过时间t后,物体下落一段高度,速率仍为υ,方向与初速度相反,如图所示.在这一运动过程中,下列关于风力做功的说法,正确的是( )
将质量为m的物体在高空中以速率υ水平向右抛出,由于风力作用,经过时间t后,物体下落一段高度,速率仍为υ,方向与初速度相反,如图所示.在这一运动过程中,下列关于风力做功的说法,正确的是( )| A. | 风力对物体不做功 | |
| B. | 风力对物体做的功(绝对值)为$\frac{{m{g^2}{t^2}}}{2}$ | |
| C. | 风力对物体做的功(绝对值)小于$\frac{{m{g^2}{t^2}}}{2}$ | |
| D. | 由于风力方向未知,不能判断风力做功情况 |
17. 云台山是全球首批世界地质公园,青龙峡景点有“中原第一峡谷”美誉,这里气候独特,植被原始完整,是生态旅游的好去处,乘坐索道缆车观赏怡人的风景以外,还能感觉悬挂在高空的刺激感.对于正在乘坐索道缆车观光的某游客来说,以下说法正确的是( )
云台山是全球首批世界地质公园,青龙峡景点有“中原第一峡谷”美誉,这里气候独特,植被原始完整,是生态旅游的好去处,乘坐索道缆车观赏怡人的风景以外,还能感觉悬挂在高空的刺激感.对于正在乘坐索道缆车观光的某游客来说,以下说法正确的是( )
 云台山是全球首批世界地质公园,青龙峡景点有“中原第一峡谷”美誉,这里气候独特,植被原始完整,是生态旅游的好去处,乘坐索道缆车观赏怡人的风景以外,还能感觉悬挂在高空的刺激感.对于正在乘坐索道缆车观光的某游客来说,以下说法正确的是( )
云台山是全球首批世界地质公园,青龙峡景点有“中原第一峡谷”美誉,这里气候独特,植被原始完整,是生态旅游的好去处,乘坐索道缆车观赏怡人的风景以外,还能感觉悬挂在高空的刺激感.对于正在乘坐索道缆车观光的某游客来说,以下说法正确的是( )| A. | 以自己为参考系,看到同一缆车里的人向对面的山不断靠近 | |
| B. | 以对面的山为参考系,自己静止不动 | |
| C. | 以所乘坐的缆车为参考系,看到两边的绿树在向前运动 | |
| D. | 以自己为参考系,看到对面的山迎面而来 |
 如图所示,两个物体A、B受到的重力分别为200N和150N,定滑轮光滑,物体均处于静止状态.试求:
如图所示,两个物体A、B受到的重力分别为200N和150N,定滑轮光滑,物体均处于静止状态.试求: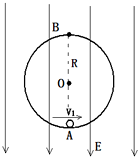 如图所示,内表面光滑绝缘的半径为1.2m的圆形轨道处于竖直平面内,有竖直向下的匀强电场,场强大小为3×106V/m.有一质量为0.12kg、带负电的小球,电荷量大小为1.6×10-6C,小球在圆轨道内壁做圆周运动,当运动到最低点A时,小球与轨道压力恰好为零,g取10m/s2,求:
如图所示,内表面光滑绝缘的半径为1.2m的圆形轨道处于竖直平面内,有竖直向下的匀强电场,场强大小为3×106V/m.有一质量为0.12kg、带负电的小球,电荷量大小为1.6×10-6C,小球在圆轨道内壁做圆周运动,当运动到最低点A时,小球与轨道压力恰好为零,g取10m/s2,求: