题目内容
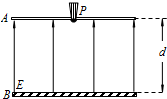 静电喷漆技术具有效率高,浪费少,质量好,有利于工人健康等优点,其装置示意图如图所示.A、B为两块平行金属板,间距d=0.30m,两板间有方向由B指向A、电场强度E=1.0×103N/C的匀强电场.在A板的中央放置一个安全接地的静电油漆喷枪P,油漆喷枪的半圆形喷嘴可向各个方向均匀地喷出带电油漆微粒,油漆微粒的质量m=2.0×10-15kg、电荷量为q=-2.0×10-16C,喷出的初速度v0=2.0m/s.油漆微粒最后都落在金属板B上.微粒所受重力和空气阻力以及微粒之间的相互作用力均可忽略.试求:
静电喷漆技术具有效率高,浪费少,质量好,有利于工人健康等优点,其装置示意图如图所示.A、B为两块平行金属板,间距d=0.30m,两板间有方向由B指向A、电场强度E=1.0×103N/C的匀强电场.在A板的中央放置一个安全接地的静电油漆喷枪P,油漆喷枪的半圆形喷嘴可向各个方向均匀地喷出带电油漆微粒,油漆微粒的质量m=2.0×10-15kg、电荷量为q=-2.0×10-16C,喷出的初速度v0=2.0m/s.油漆微粒最后都落在金属板B上.微粒所受重力和空气阻力以及微粒之间的相互作用力均可忽略.试求:(1)微粒落在B板上的动能;
(2)微粒从离开喷枪后到达B板所需的最短时间;
(3)微粒最后落在B板上所形成图形的面积.
分析:(1)微粒从喷出到落在B板上的过程,电场力做正功,根据动能定理求解.
(2)微粒初速度方向垂直于极板时,到达B板时间最短.由动能求出微粒打在B板上的速度,由运动公式求出最短时间.
(3)微粒落在B板上所形成的图形是圆形,对于喷枪沿垂直电场方向喷出的油漆微粒落在圆的边界上.根据运动的分解研究垂直电场方向喷出的油漆微粒,由牛顿定律和运动常规规律求出圆的半径,再求圆的面积.
(2)微粒初速度方向垂直于极板时,到达B板时间最短.由动能求出微粒打在B板上的速度,由运动公式求出最短时间.
(3)微粒落在B板上所形成的图形是圆形,对于喷枪沿垂直电场方向喷出的油漆微粒落在圆的边界上.根据运动的分解研究垂直电场方向喷出的油漆微粒,由牛顿定律和运动常规规律求出圆的半径,再求圆的面积.
解答:解:(1)据动能定理,电场力对每个微粒做功W=Ekt-Ek0=qEd,
微粒打在B板上时的动能 Ekt=W+Ek0=qEd+
m
代入数据解得:Ekt=6.4×10-14J
(2)微粒初速度方向垂直于极板时,到达B板时间最短,到达B板时速度为vt,有Ekt=
m
可得vt=8.0m/s.
由于微粒在两极板间做匀加速运动,即
=
可解得 t=0.06s
(3)由于喷枪喷出的油漆微粒是向各个方向,因此微粒落在B板上所形成的图形是圆形.对于喷枪沿垂直电场方向喷出的油漆微粒,在电场中做抛物线运动,根据牛顿第二定律,油漆颗粒沿电场方向运动的加速度 a=
运动的位移 d=
at12
油漆颗粒沿垂直于电场方向做匀速运动,运动的位移即为落在B板上圆周的半径R=v0t1
微粒最后落在B板上所形成的圆面积 S=πR2
联立以上各式,得 S=
代入数据解得 S=7.5ⅹ10-2m2
答:(1)微粒落在B板上的动能为6.4×10-14J;
(2)微粒从离开喷枪后到达B板所需的最短时间为0.06s;
(3)微粒最后落在B板上所形成图形的面积为7.5ⅹ10-2m2.
微粒打在B板上时的动能 Ekt=W+Ek0=qEd+
| 1 |
| 2 |
| v | 2 0 |
代入数据解得:Ekt=6.4×10-14J
(2)微粒初速度方向垂直于极板时,到达B板时间最短,到达B板时速度为vt,有Ekt=
| 1 |
| 2 |
| v | 2 t |
可得vt=8.0m/s.
由于微粒在两极板间做匀加速运动,即
| d |
| t |
| v0+vt |
| 2 |
可解得 t=0.06s
(3)由于喷枪喷出的油漆微粒是向各个方向,因此微粒落在B板上所形成的图形是圆形.对于喷枪沿垂直电场方向喷出的油漆微粒,在电场中做抛物线运动,根据牛顿第二定律,油漆颗粒沿电场方向运动的加速度 a=
| Eq |
| m |
运动的位移 d=
| 1 |
| 2 |
油漆颗粒沿垂直于电场方向做匀速运动,运动的位移即为落在B板上圆周的半径R=v0t1
微粒最后落在B板上所形成的圆面积 S=πR2
联立以上各式,得 S=
2πmd
| ||
| qE |
代入数据解得 S=7.5ⅹ10-2m2
答:(1)微粒落在B板上的动能为6.4×10-14J;
(2)微粒从离开喷枪后到达B板所需的最短时间为0.06s;
(3)微粒最后落在B板上所形成图形的面积为7.5ⅹ10-2m2.
点评:本题是实际问题,考查理论联系实际的能力,关键在于建立物理模型.第(3)问要弄清物理情景,实质是研究类平抛运动问题.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
 静电喷漆技术具有效率高、质量好、有益于健康等优点,其装置可简化如图.A、B为有一定间距的两块平行金属板,两板间有方向由B指向A的匀强电场.在A板的中央放置一个安全接地的静电油漆喷枪P,油漆喷枪可向各个方向均匀地喷出初速度大小相同且带负电的油漆微粒,假设油漆微粒的质量、电荷量大小均相等,微粒的重力和所受空气阻力均不计,油漆微粒最后都能落在金属板B上.对油漆微粒,下列说法正确的是( )
静电喷漆技术具有效率高、质量好、有益于健康等优点,其装置可简化如图.A、B为有一定间距的两块平行金属板,两板间有方向由B指向A的匀强电场.在A板的中央放置一个安全接地的静电油漆喷枪P,油漆喷枪可向各个方向均匀地喷出初速度大小相同且带负电的油漆微粒,假设油漆微粒的质量、电荷量大小均相等,微粒的重力和所受空气阻力均不计,油漆微粒最后都能落在金属板B上.对油漆微粒,下列说法正确的是( ) 静电喷漆技术具有效率高,浪费少,质量好,有利于工人健康等优点,其装置如图所示.A、B为两块平行金属板,间距d=0.50m,两板间有方向由B指向A,大小为E=l.0×l03N/C的匀强电场.在A板的中央放置一个安全接地的静电油漆喷枪P.油漆喷枪的半圆形喷嘴可向各个方向均匀地喷出带电油漆微粒,油漆微粒的初速度大小均为vo=2.0m/s,质量m=5.0×l0-16kg、带电量为q=-2.0×10-16C.微粒的重力和所受空气阻力均不计,油漆微粒最后都落在金属板B上.试求:
静电喷漆技术具有效率高,浪费少,质量好,有利于工人健康等优点,其装置如图所示.A、B为两块平行金属板,间距d=0.50m,两板间有方向由B指向A,大小为E=l.0×l03N/C的匀强电场.在A板的中央放置一个安全接地的静电油漆喷枪P.油漆喷枪的半圆形喷嘴可向各个方向均匀地喷出带电油漆微粒,油漆微粒的初速度大小均为vo=2.0m/s,质量m=5.0×l0-16kg、带电量为q=-2.0×10-16C.微粒的重力和所受空气阻力均不计,油漆微粒最后都落在金属板B上.试求:
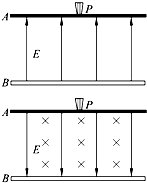 静电喷漆技术具有效率高、质量好、有益于健康等优点,其装置可简化如图.A、B为水平放置的间距d=0.9m的两块足够大的平行金属板,两板间有方向由B指向A的匀强电场,电场强度为E=0.1V/m.在A板的中央放置一个安全接地的静电油漆喷枪P,油漆喷枪可向各个方向均匀地喷出初速度大小均为v0=8m/s的油漆微粒,已知油漆微粒的质量均为m=1×10-5 kg、电荷量均为q=-1×10-3 C不计空气阻力,油漆微粒最后都能落在金属板B上.
静电喷漆技术具有效率高、质量好、有益于健康等优点,其装置可简化如图.A、B为水平放置的间距d=0.9m的两块足够大的平行金属板,两板间有方向由B指向A的匀强电场,电场强度为E=0.1V/m.在A板的中央放置一个安全接地的静电油漆喷枪P,油漆喷枪可向各个方向均匀地喷出初速度大小均为v0=8m/s的油漆微粒,已知油漆微粒的质量均为m=1×10-5 kg、电荷量均为q=-1×10-3 C不计空气阻力,油漆微粒最后都能落在金属板B上.