题目内容
(2013?天津模拟)静电喷漆技术具有效率高、浪费少、质量好、有益于健康等优点,其装置可简化如图.A、B为水平放置的间距d=1.6m的两块足够大的平行金属板,两板间有方向由B指向A的匀强电场,场强为E=0.1v/m.在A板的中央放置一个安全接地的静电油漆喷枪P,油漆喷枪可向各个方向均匀地喷出初速度大小均为v0=6m/s的油漆微粒,已知油漆微粒的质量均为m=1.0×10-5kg、电荷量均为q=-1.0×10-3C,不计油漆微粒间的相互作用、油漆微粒带电对板间电场和磁场的影响及空气阻力,重力加速度g=10m/s2.求:
(1)油漆微粒落在B板上所形成的图形面积;
(2)若让A、B两板间的电场反向,并在两板间加垂直于纸面向里的匀强磁场,磁感应强度B=0.06T,调节喷枪使油漆微粒只能在纸面内沿各个方向喷出,其它条件不变.B板被油漆微粒打中的区域的长度;
(3)在满足(2)的情况下,打中B板的油漆微粒中,在磁场中运动的最短时间.

(1)油漆微粒落在B板上所形成的图形面积;
(2)若让A、B两板间的电场反向,并在两板间加垂直于纸面向里的匀强磁场,磁感应强度B=0.06T,调节喷枪使油漆微粒只能在纸面内沿各个方向喷出,其它条件不变.B板被油漆微粒打中的区域的长度;
(3)在满足(2)的情况下,打中B板的油漆微粒中,在磁场中运动的最短时间.

分析:(1)根据牛顿第二定律与运动学公式,结合圆形面积公式,即可求解;
(2)根据重力与电场力相平衡,由牛顿第二定律,结合洛伦兹力提供向心力,与几何知识,即可求解;
(3)根据打在B板上的微粒中,pc最短的弦长对应的时间最短,结合几何关系,与周期公式,即可求解.
(2)根据重力与电场力相平衡,由牛顿第二定律,结合洛伦兹力提供向心力,与几何知识,即可求解;
(3)根据打在B板上的微粒中,pc最短的弦长对应的时间最短,结合几何关系,与周期公式,即可求解.
解答:解:(1)油漆微粒的加速度为:a=
…①
根据运动学公式有:d=
at2…②
运动的半径:x=v0t…③
落在B板上所形成圆形面积为:s=πx2…④
由①②③式并代入数据得:s=18.1m2…⑤
(2)当电场反向是有:Eq=mg…⑥
油漆微粒做匀速圆周运动,洛伦兹力充当向心力,由牛顿第二定律有:Bqv=m
…⑦
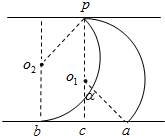
水平向右射出的油漆微粒打在B板的右端,根据几何关系有:R+Rcosα=d…⑧
ac的长度为:ac=Rsinα…⑨
打在B板左端的油漆微粒为和板相切的微粒,同理求得:bc=ac…⑩
油漆微粒打在极板上的长度为:ab=ac+bc…(11)
由⑥⑦⑧⑨⑩(11)式并代入数据得:ab=1.6m…(12)
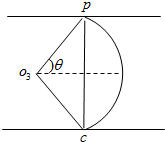
(3)打在B板上的微粒中,pc最短的弦长对应的时间最短,
由几何关系有:sinθ=
…(13)
运动的最短时间为:tmin=
T…(14)
微粒在磁场中运动的周期为:T=
…(15)
由⑦(13)(15)式代入数据解得:tmin=0.31s;
答:(1)油漆微粒落在B板上所形成的图形面积s=18.1m2;
(2)若让A、B两板间的电场反向,并在两板间加垂直于纸面向里的匀强磁场,磁感应强度B=0.06T,调节喷枪使油漆微粒只能在纸面内沿各个方向喷出,其它条件不变.B板被油漆微粒打中的区域的长度ab=1.6m;
(3)在满足(2)的情况下,打中B板的油漆微粒中,在磁场中运动的最短时间0.31s.
| Eq+mg |
| m |
根据运动学公式有:d=
| 1 |
| 2 |
运动的半径:x=v0t…③
落在B板上所形成圆形面积为:s=πx2…④
由①②③式并代入数据得:s=18.1m2…⑤
(2)当电场反向是有:Eq=mg…⑥
油漆微粒做匀速圆周运动,洛伦兹力充当向心力,由牛顿第二定律有:Bqv=m
| v2 |
| R |

水平向右射出的油漆微粒打在B板的右端,根据几何关系有:R+Rcosα=d…⑧
ac的长度为:ac=Rsinα…⑨
打在B板左端的油漆微粒为和板相切的微粒,同理求得:bc=ac…⑩
油漆微粒打在极板上的长度为:ab=ac+bc…(11)
由⑥⑦⑧⑨⑩(11)式并代入数据得:ab=1.6m…(12)
(3)打在B板上的微粒中,pc最短的弦长对应的时间最短,
由几何关系有:sinθ=
| ||
| R |
运动的最短时间为:tmin=
| 2θ |
| 2π |

微粒在磁场中运动的周期为:T=
| 2πm |
| Bq |
由⑦(13)(15)式代入数据解得:tmin=0.31s;
答:(1)油漆微粒落在B板上所形成的图形面积s=18.1m2;
(2)若让A、B两板间的电场反向,并在两板间加垂直于纸面向里的匀强磁场,磁感应强度B=0.06T,调节喷枪使油漆微粒只能在纸面内沿各个方向喷出,其它条件不变.B板被油漆微粒打中的区域的长度ab=1.6m;
(3)在满足(2)的情况下,打中B板的油漆微粒中,在磁场中运动的最短时间0.31s.
点评:考查带电粒子在磁场中做匀速圆周运动,掌握牛顿第二定律与运动学公式的综合应用,理解几何关系在题中的运用,注意会画出运动轨道,及已知长度与半径的半径.

练习册系列答案
相关题目
 (2013?天津模拟)如图所示,MN和PQ为固定在绝缘水平面上两平行光滑金属导轨,导轨左端MP间接有阻值为R1=2Ω导线;导轨右端接有与水平轨道相切、半径r=0.5m内壁光滑的半圆金属轨道.导轨间距L=0.4m,电阻不计.导轨所在平面abcd区域内有竖直向上B=0.5T的匀强磁场.导轨上长度也为0.4m、质量m=0.6kg、电阻R2=1Ω的金属棒AB以v0=6m/s速度进入磁场区域,离开磁场区域后恰好能到达半圆轨道的最高点,运动中金属棒始终与导轨保持良好接触.已知重力加速度g=10m/s2.求:
(2013?天津模拟)如图所示,MN和PQ为固定在绝缘水平面上两平行光滑金属导轨,导轨左端MP间接有阻值为R1=2Ω导线;导轨右端接有与水平轨道相切、半径r=0.5m内壁光滑的半圆金属轨道.导轨间距L=0.4m,电阻不计.导轨所在平面abcd区域内有竖直向上B=0.5T的匀强磁场.导轨上长度也为0.4m、质量m=0.6kg、电阻R2=1Ω的金属棒AB以v0=6m/s速度进入磁场区域,离开磁场区域后恰好能到达半圆轨道的最高点,运动中金属棒始终与导轨保持良好接触.已知重力加速度g=10m/s2.求: