题目内容
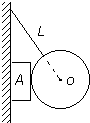
如图所示,光滑匀质圆球的直径为40厘米,质量为20千克,悬线长L=30厘米,正方形物体A厚10厘米,质量为2千克,物块A与墙之间的摩擦因数μ=0.2,取g=10米/秒2.问:
(1)墙对A的摩擦力多大?
(2)如果在物块A上施加一个与墙平行的外力F,使A在未脱离圆球前贴着墙沿水平向纸内方向作加速度a=5米/秒2的匀加速直线运动,那么这个外力F的大小、方向如何?
(1)墙对A的摩擦力多大?
(2)如果在物块A上施加一个与墙平行的外力F,使A在未脱离圆球前贴着墙沿水平向纸内方向作加速度a=5米/秒2的匀加速直线运动,那么这个外力F的大小、方向如何?

(1)对物块A受力分析,受重力、静摩擦力、球对其向左的压力、墙壁对其向右的支持力,如图
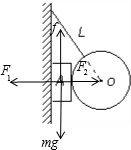
根据平衡条件,有:
f静=mg=20N;
(1)先对球受力分析,受重力、支持力和拉力,如图
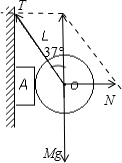
根据平衡条件,有
N=Mgtan37°=
Mg=150N;
故A对墙壁的压力也为150N,A与墙壁间的滑动摩擦力为:f=μN=0.2×150=30N;
物体A匀速运动,平行墙壁的竖直面内受重力、弹力和滑动摩擦力,如图
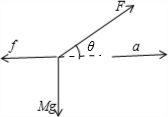
根据牛顿第二定律,有:
水平方向:Fcosθ-f=ma
竖直方向:Fsinθ-mg=0
解得:F=20
N≈44.72N;
θ=arctan
;
答:(1)墙对A的摩擦力为20N;
(2)这个外力F的大小为44.72N,与水平方向成arctan
角度斜向上.

根据平衡条件,有:
f静=mg=20N;
(1)先对球受力分析,受重力、支持力和拉力,如图

根据平衡条件,有
N=Mgtan37°=
| 3 |
| 4 |
故A对墙壁的压力也为150N,A与墙壁间的滑动摩擦力为:f=μN=0.2×150=30N;
物体A匀速运动,平行墙壁的竖直面内受重力、弹力和滑动摩擦力,如图

根据牛顿第二定律,有:
水平方向:Fcosθ-f=ma
竖直方向:Fsinθ-mg=0
解得:F=20
| 5 |
θ=arctan
| 1 |
| 2 |
答:(1)墙对A的摩擦力为20N;
(2)这个外力F的大小为44.72N,与水平方向成arctan
| 1 |
| 2 |

练习册系列答案
相关题目







