题目内容
19.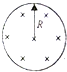 如图所示圆形区域中有垂直圆面,磁感应强度为B的匀强磁场,在圆心位置有一β粒子(质量为m,电量为-e)放射源,沿圆面向各个方向释放最大速度为v的β粒子,欲使β粒子约束在圆形磁场区内而不射出,则此圆形区域最小半径为( )
如图所示圆形区域中有垂直圆面,磁感应强度为B的匀强磁场,在圆心位置有一β粒子(质量为m,电量为-e)放射源,沿圆面向各个方向释放最大速度为v的β粒子,欲使β粒子约束在圆形磁场区内而不射出,则此圆形区域最小半径为( )| A. | $\frac{mv}{eB}$ | B. | $\frac{2mv}{eB}$ | C. | $\frac{mv}{2eB}$ | D. | $\frac{4mv}{eB}$ |
分析 β粒子在磁场中做匀速圆周运动,粒子速度越大粒子轨道半径越大,速度最大的粒子运动轨迹恰好与磁场边界相切时对应的粒子轨道半径最大,求出此时磁场区域半径,然后分析答题.
解答 解:β粒子在磁场中做匀速圆周运动,洛伦兹力提供向心力,由牛顿第二定律得:evB=m$\frac{{v}^{2}}{r}$,
解得:r=$\frac{mv}{eB}$,
β粒子恰好不离开磁场区域时,磁场区域的半径:R=2r=$\frac{2mv}{eB}$,
则使β粒子约束在圆形磁场区内而不射出,则此圆形区域最小半径为$\frac{2mv}{eB}$;
故选:B.
点评 本题考查了粒子在磁场中的运动,分析清楚粒子运动过程是正确解题的关键,应用牛顿第二定律可以解题.

练习册系列答案
 每课必练系列答案
每课必练系列答案
相关题目
10. 如图所示,一根长的、不可伸长的柔软轻绳跨过光滑定滑轮,绳的两端各系一个小球a和b,a球的质量为m,静置于水平地面;b球的质量为M,用手托住,距地面的高度为h,此时轻绳刚好拉紧,从静止释放b后,a达到的最大高度为1.5h,则M、m的比值为( )
如图所示,一根长的、不可伸长的柔软轻绳跨过光滑定滑轮,绳的两端各系一个小球a和b,a球的质量为m,静置于水平地面;b球的质量为M,用手托住,距地面的高度为h,此时轻绳刚好拉紧,从静止释放b后,a达到的最大高度为1.5h,则M、m的比值为( )
 如图所示,一根长的、不可伸长的柔软轻绳跨过光滑定滑轮,绳的两端各系一个小球a和b,a球的质量为m,静置于水平地面;b球的质量为M,用手托住,距地面的高度为h,此时轻绳刚好拉紧,从静止释放b后,a达到的最大高度为1.5h,则M、m的比值为( )
如图所示,一根长的、不可伸长的柔软轻绳跨过光滑定滑轮,绳的两端各系一个小球a和b,a球的质量为m,静置于水平地面;b球的质量为M,用手托住,距地面的高度为h,此时轻绳刚好拉紧,从静止释放b后,a达到的最大高度为1.5h,则M、m的比值为( )| A. | 5:4 | B. | 5:3 | C. | 3:1 | D. | 3:2 |
14.如图所示是某导体的I-U图线,图中α=45°,下列说法正确的是( )
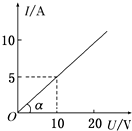

| A. | 此导体的电阻R=0.5Ω | |
| B. | 通过电阻的电流与其两端的电压成正比 | |
| C. | IU图线的斜率表示电阻的倒数,所以R=cot45°=1.0Ω | |
| D. | 在R两端加6.0 V电压时,每秒通过电阻截面的电荷量是3.0C |
8.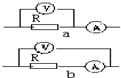 用伏安法测电阻的实验,可以采用图示a、b两种方法把伏特表和安培表连人电路,这样测量出来的电阻值与被测电阻的真实阻值比较,下列正确的是( )
用伏安法测电阻的实验,可以采用图示a、b两种方法把伏特表和安培表连人电路,这样测量出来的电阻值与被测电阻的真实阻值比较,下列正确的是( )
 用伏安法测电阻的实验,可以采用图示a、b两种方法把伏特表和安培表连人电路,这样测量出来的电阻值与被测电阻的真实阻值比较,下列正确的是( )
用伏安法测电阻的实验,可以采用图示a、b两种方法把伏特表和安培表连人电路,这样测量出来的电阻值与被测电阻的真实阻值比较,下列正确的是( )| A. | 两种接法的测量值都小于真实值 | B. | 采用a图接法,测量值小于真实值 | ||
| C. | 采用b图接法,测量值大于真实值 | D. | 两种接法的测量值都大于真实值 |
