题目内容
【题目】高H=5m的光滑水平台左端水平放置一两轮间距d=6.0m的传送带。可视为质点的滑块a、b之间用细绳相连,其间有一处于压缩状态的轻质弹簧(滑块与弹簧不拴接),开始时整个装置处于静止状态。某时刻装置中的细线忽然断开,滑块a、b被弹出,其中滑块a以速度v0=5.0m/s向左滑上传送带,滑块b沿竖直放置的半径为R=0.1m的光滑圆形管道做圆周运动,并通过最高点C。已知滑块a、b的质量分别为ma=1.0kg,mb=2.0kg,传送带逆时针转动,滑块a与传送带之间的动摩擦因数![]() =0.2,空气阻力不计,g=10m/s2。求:
=0.2,空气阻力不计,g=10m/s2。求:

(1)滑块a、b被弹出时,滑块b的速度vb及细绳断开前弹簧弹性势能Ep;
(2)滑块b通过圆形管道最高点时对管道的压力;
(3)试分析传送带的速度满足什么条件时,滑块a离开传送带左边缘落地的水平距离最大,并求出最大距离。
【答案】(1)2.5m/s;18.75J;(2)滑块b对管道上壁有向上的压力,大小为25N;(3)7m
【解析】
(1)弹开前后,a、b系统动量守恒:mav0=mbv
解得:vb=2.5m/s
又由能量守恒知,弹簧弹性势能:Ep=![]() mav02+
mav02+![]() mbvb2=18.75J
mbvb2=18.75J
(2)滑块b通过圆形管道到最高点C过程,根据机械能守恒有:![]() mbvb2-
mbvb2-![]() mbvc2=mbg2R
mbvc2=mbg2R
在最高点处,由牛顿第二定律有:mbg+Fc=mb![]()
解得:Fc=25N
又由牛顿第三定律知:滑块b对管道上壁有向上的压力,大小为25N。
(3)经分析知,若传送带逆时针转动,且滑块a能一直匀加速运动直至平抛出,滑块a离开传送带左边缘落地的水平距离最大。滑块a在传送带上匀加速运动:a=![]() g=2m/s2
g=2m/s2
设出传送带时速度为va,则由运动学公式有:va2-v02=2ad
解得:va=7m/s
故当传送带时速度v![]() 7m/s时,滑块a离开传送带左边缘落地的水平距离最大。
7m/s时,滑块a离开传送带左边缘落地的水平距离最大。
由平抛规律有:H=![]() gt2
gt2
x=vat
解得最大水平距离:x=7m

 开心蛙口算题卡系列答案
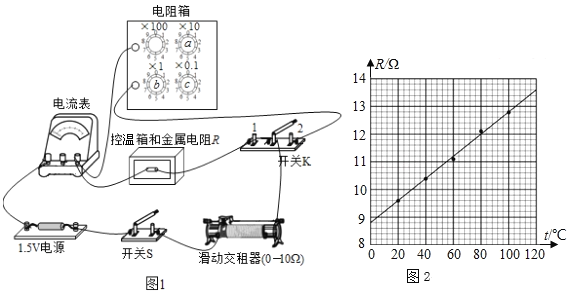
开心蛙口算题卡系列答案【题目】实验小组利用变阻箱和一个电流表研究小灯泡工作时的电阻与电流间的关系,设计电路如图a所示.开关S闭合前,滑动变阻器的滑片滑到a端,变阻器R的阻值调到最大位置.
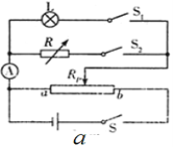
(1)①调节RP,使得测量电路的电压由较低电压开始.先闭合S1,断开S2,记录电流I1;再断开S1,闭合S2,调节____________,使电流表读数也为I1,并记录R的阻值R1.
②逐次调节________,改变测量电路电压,重复①的测量,得I1、I2、I3、I4…,R1、R2、R3、R4….
(2)利用测得的数据,在图b所示坐标纸上画出R-I图象__________;
电流(A) | 0.00 | 0.10 | 0.20 | 0.30 | 0.36 | 0.39 | 0.41 | 0.43 |
电阻(Ω) | 2.50 | 2.50 | 3.33 | 4.17 | 5.13 | 6.10 | 6.98 |
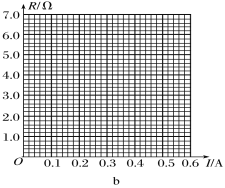
(3)根据图象判断,当流过的电流为0.40A时,灯丝电阻约为________.