题目内容
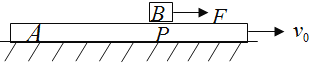
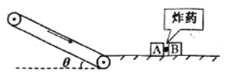
【题目】如图所示，可视为质点的滑块A、B静止在光滑水平地面上，A、B滑块的质量分别为mA=1kg，mB=3kg。在水平地面左侧有倾角θ=30°的粗糙传送带以v=6m/s的速率顺时针匀速转动传送带与光滑水平面通过半径可忽略的光滑小圆弧平滑连接A、B两滑块间夹着质量可忽略的炸药，现点燃炸药爆炸瞬间，滑块A以6m/s水平向左冲出，接着沿传送带向上运动，已知滑块A与传送带间的动摩擦因数为μ=
，传送带与水平面足够长重力加速度g取10m/s2
(1)求滑块A沿传送带上滑的最大距离；
(2)若滑块A滑下后与滑块B相碰并粘住，求A、B碰撞过程中损失的能量△E；
(3)求滑块A与传送带接触过程中因摩擦产生的热量Q
【答案】(1) 
(2) 
(3) 
【解析】
爆炸过程，对A和B组成的系统由动量守恒，求出爆炸后B的速度；水平地面光滑，滑块A沿传送带向上的做匀减速直线运动，根据牛顿第二定律和运动学公式求出滑块A沿传送带向上减速到零通过的距离；当滑块A速度减为零后，当滑块A速度减为零后，经t2=0.6s滑块A与传送带共速，A刚好回到传送带与水平面的的连接点，当滑块A再次滑上水平面，滑块A与滑块B碰撞时，粘连在一起,对A、B组成的系统由动量守恒定律解得共同的速度，根据能量守恒求得碰撞过程中损失的能量；分别求出滑块A向上运动和向下运动过程中产生的热量，再求出滑块A与传送带接触过程中因摩擦产生的热量；
解：(1)设爆炸后A、B的速度分别为
、
，爆炸过程，对A和B组成的系统由动量守恒有：
解得：
水平地面光滑，滑块A沿传送带向上的做匀减速直线运动，对A进行受力分析有： 
解得：
经t1=0.6s滑块A速度减为0
故滑块A沿传送带向上减速到零通过的距离为：
(2)当滑块A速度减为零后，滑块A将沿传送带向下做匀加速运动，对A进行受力分析有：
经t2=0.6s滑块A与传送带共速
根据对称性可知滑块A刚好回到传送带与水平面的的连接点
当滑块A再次滑上水平面时，速度大小与传送速度相等为6m/s
滑块A与滑块B碰撞时，粘连在一起,对A、B组成的系统
由动量守恒定律得：
解得：
碰撞过程中损失的能量为
代入数据得：
(3)经t1=0.6s滑块A速度减为零滑块A沿传送带向上减速到零通过的位移：
此过程中传送带的位移：
滑块A速度减为零后将沿传送带向下做匀加速运动，经t2=0.6s滑块A与传送带共速，达到共速时传送带的位移：
传送带的位移
若向上运动和向下运动过程中产生的热量分别为Q1、Q2，则由
得：
故因摩擦产生的热量
