题目内容
20.如图(甲)所示,倾角为θ=30°的光滑固定斜杆底端固定一个带负电、电量为Q=2×10-4C的小球A,将一可视为质点的带电小球B从斜杆的底端a点(与A靠得很近,但未接触)静止释放,小球沿斜面向上滑动过程中速度v随位移s的变化图象如图(乙)所示.已知重力加速度g=10m/s2,静电力常量k=9×109N•m2/C2. 求: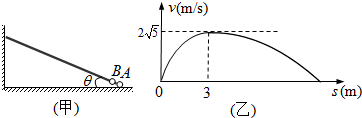
(1)小球B的荷质比$\frac{q}{m}$;
(2)小球B在b点时速度到达最大,求a、b两点的电势差Uab.
分析 (1)由v-s图知道在s0=3m时,小球的速度达到最大,为v=2$\sqrt{5}$m/s,此时小球受力平衡,由平衡条件和库仑定律结合求比荷.
(2)对小球从释放到速度最大的过程,运用动能定理列式,可求电势差Uab.
解答 解:(1)由v-s图知,在s0=3m时,小球的速度最大为v=2$\sqrt{5}$m/s,受力平衡,即有
mgsinθ=k$\frac{qQ}{{s}_{0}^{2}}$ ①
所以小球B带负电,比荷$\frac{q}{m}$=2.5×10-5C/kg
(2)对小球从释放到速度最大的过程,由动能定理得:
-qUab-mgs0sinθ=$\frac{1}{2}m{v}^{2}$ ②
解得:Uab=-1×106V
答:
(1)小球B的荷质比$\frac{q}{m}$是2.5×10-5C/kg;
(2)小球B在b点时速度到达最大,a、b两点的电势差Uab为-1×106V.
点评 本题首先要抓住图象的信息,分析小球的运动情况,再根据平衡条件和动能定理进行处理.

练习册系列答案
相关题目
10.一正方形金属线框位于有界匀强磁场区域内,线框平面与磁场垂直,线框的右边紧贴着磁场边界,如图甲所示.t=0时刻对线框施加一水平向右的外力F,让线框从静止开始做匀加速直线运动穿过磁场.外力F随时间t变化的图线如图乙所示.已知线框质量m=1kg、电阻R=1Ω.以下说法正确的是( )
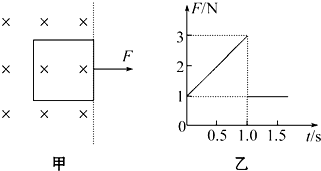

| A. | 匀强磁场的磁感应强度为2T | |
| B. | 线圈做匀加速直线运动的加速度为1m/s2 | |
| C. | 线框穿过磁场的过程中,通过线框的电荷量为$\frac{\sqrt{2}}{2}$C | |
| D. | 线框穿过磁场的过程中,线框上产生的焦耳热为1.5J |
11.每到夏季,我省各地纷纷进入雨季,雷雨等强对流天气频繁发生.当我们遇到雷雨天气时,一定要注意避防雷电.下列说法正确的是( )
①固定电话和手提电话均可正常使用
②不要接触天线、金属门窗、建筑物外墙,远离带电设备
③不宜使用无防雷措施的电器或防雷措施不足的电器及水龙头
④在旷野,应远离树木和电线杆.
①固定电话和手提电话均可正常使用
②不要接触天线、金属门窗、建筑物外墙,远离带电设备
③不宜使用无防雷措施的电器或防雷措施不足的电器及水龙头
④在旷野,应远离树木和电线杆.
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
15.下列说法中正确的是( )
| A. | 在空中将物体释放后,物体不受重力作用 | |
| B. | 物体向上运动时所受的重力比向下运动时所受的重力大 | |
| C. | 物体重心的位置与物体的形状无关 | |
| D. | 在地球上方的物体都要受到重力作用,不管是否存在其他力的作用 |
12.一个恒力F作用在物体上,使物体在力的方向上发生了一段位移s,下面关于力F做的功的说法正确的是( )
| A. | 物体加速运动时,力F做的功最多 | |
| B. | 物体匀速运动时,力F做的功最多 | |
| C. | 物体匀减速运动时,力F的功最少 | |
| D. | 力F对物体做功与物体运动快慢无关 |
9.下列说法正确的是( )
| A. | 卢瑟福由α粒子散射实验提出了原子的核式结构 | |
| B. | 康普顿发现了电子 | |
| C. | 人类认识原子核的复杂结构是从天然放射现象开始的 | |
| D. | β射线是原子核外的电子电离形成的电子流,它具有中等的穿透能力 | |
| E. | 根据玻尔理论可知,氢原子辐射出一个光子后,氢原子的电势能增大,核外电子动能增大,总能量增大 | |
| F. | 在光电效应的实验中,入射光的强度增大,光电子的最大初动能也增大 |
19.某同学选用如图1所示的装置做“测定匀变速直线运动的加速度”的实验,电源的频率为50Hz.
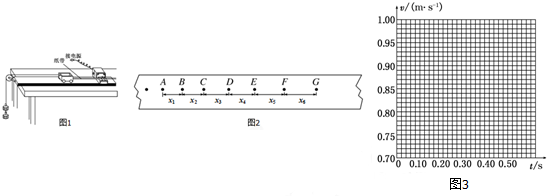
(1)该同学根据打出的纸带认为不用计算就能直接得到的物理量有两个,请帮他选出AB
A、时间间隔 B、位移 C、加速度 D、平均速度
(2)该同学选出了一条的清晰纸带,并根据纸带上的点,标出了如图2所示的计数点,其中两相邻计数点间还有4个点未画出,x1=7.05cm,x2=7.68cm,x3=8.33cm,x4=8.95cm,x5=9.61cm,x6=10.26cm.上表列出了打点计时器打下B、C、F时小车的瞬时速度,请在表中填入打点计时器打下D、E两点时小车的瞬时速度.
(4)根据(3)问的数据,以A点为计时起点,在图3中画出小车的速度-时间关系图线,并利用图象求出小车的加速度大小为0.64m/s2.

(1)该同学根据打出的纸带认为不用计算就能直接得到的物理量有两个,请帮他选出AB
A、时间间隔 B、位移 C、加速度 D、平均速度
(2)该同学选出了一条的清晰纸带,并根据纸带上的点,标出了如图2所示的计数点,其中两相邻计数点间还有4个点未画出,x1=7.05cm,x2=7.68cm,x3=8.33cm,x4=8.95cm,x5=9.61cm,x6=10.26cm.上表列出了打点计时器打下B、C、F时小车的瞬时速度,请在表中填入打点计时器打下D、E两点时小车的瞬时速度.
| 位置 | B | C | D | E | F |
| 速度(m/s) | 0.737 | 0.801 | 0.994 |
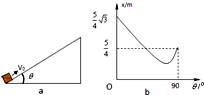 如图(a)所示,一物体以一定的速度v0沿足够长斜面向上运动,此物体在斜面上的最大位移与斜面倾角的关系由图(b)中的曲线给出.设各种条件下,物体运动过程中的摩擦系数不变.g=10m/s2试求
如图(a)所示,一物体以一定的速度v0沿足够长斜面向上运动,此物体在斜面上的最大位移与斜面倾角的关系由图(b)中的曲线给出.设各种条件下,物体运动过程中的摩擦系数不变.g=10m/s2试求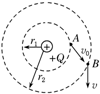 场源电荷Q=2×10-4C,是正点电荷.检验电荷q=-2×10-5C,是负点电荷,它们相距r=2m,且都在真空中,如图所示.求:
场源电荷Q=2×10-4C,是正点电荷.检验电荷q=-2×10-5C,是负点电荷,它们相距r=2m,且都在真空中,如图所示.求: