题目内容
【题目】如图所示是一个水平横截面为圆形的平底玻璃缸，玻璃缸深度为
，缸底面圆心处有一单色点光源
，缸中装有某种液体，深度为
，
点为液面的圆心，
垂直于水平面。用面积为
的黑纸片覆盖在液面上，则液面上方恰好无光线射出。若在上述黑纸片上，以为圆心剪出一个面积为
的圆孔，把余下的黑纸环仍放置在液面上原来的位置，使所有出射光线都从缸口射出，则缸口的最小面积为多少？
【答案】
【解析】
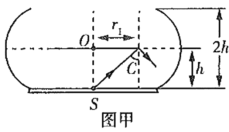
用面积为
的黑纸片覆盖在液面上，液面上方恰好无光线射出，则从点光源
发出的光线射到黑纸片的边缘处恰发生全反射，临界角为
，光路图如图甲所示。
由几何关系得
由全反射知识有
解得
剪出一个面积为
圆孔后，设透光部分的半径为
，射出光线的最大入射角为
，对应的折射角为
，光路图如图乙所示。
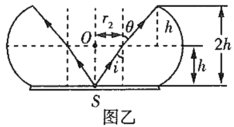
由几何关系得
根据折射定律有
缸口的最小半径为
缸口的最小面积为
解得
练习册系列答案
相关题目
