题目内容
4.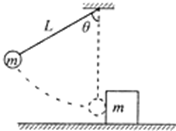 如图,质量为m的小球悬挂在长为L的细线下端,将它拉至与竖直方向成θ=60°的位置后由静止释放,当小球摆至最低点时,恰好与水平面上原来静止的、质量也为m的木块相碰,不考虑空气阻力,重力加速度为g,求:
如图,质量为m的小球悬挂在长为L的细线下端,将它拉至与竖直方向成θ=60°的位置后由静止释放,当小球摆至最低点时,恰好与水平面上原来静止的、质量也为m的木块相碰,不考虑空气阻力,重力加速度为g,求:(1)小球摆至最低点与木块碰前瞬间,小球的速度v.
(2)小球摆至最低点与木块碰前瞬间,细线的拉力F.
(3)若木块被碰后获得的速度为$\frac{4}{5}$v,木块与地面的动摩擦因数μ=$\frac{4}{25}$,求木块在水平地面上滑行的距离.
分析 (1)小球摆至最低点的过程中,绳子拉力不做功,只有重力做功,机械能守恒,即可求得小球摆至最低点时的速度v;
(2)在最低点,小球做圆周运动,重力和绳子的拉力的合力充当向心力,由牛顿第二定律求解拉力F的大小;
(3)木块被碰后获得的速度为v,木块做匀减速直线运动,由动能定理求解木块在水平地面上滑行的距离.
解答 解:(1)设小球摆至最低点时的速度为v,根据机械能守恒定律有:
mgL(1-cosθ)=$\frac{1}{2}$mv2,
小球在最低点时速度:v=$\sqrt{gL}$
(2)小球摆到最低点时,根据牛顿第二定律有:
F-mg=m$\frac{{v}^{2}}{L}$,
解得:F=2mg
(3)木块被碰后获得速度v1,在水平地面上滑行的距离为x,根据动能定理有:
$-μmgx=0-\frac{1}{2}mv_1^2$
又 v1=$\frac{4}{5}$v=$\frac{4}{5}\sqrt{gL}$
联立并代入数据,解得:x=2L
答:(1)小球摆至最低点与木块碰前瞬间,小球的速度v为$\sqrt{gL}$.
(2)小球摆至最低点与木块碰前瞬间,细线的拉力F为2mg.
(3)木块在水平地面上滑行的距离为2L.
点评 本题有三个过程:圆周运动、碰撞、匀减速运动,根据机械能守恒与牛顿第二定律的结合,是处理圆周运动动力学问题常用的方法.

练习册系列答案
相关题目
14.现代电影的拍摄中有很多的“腾云驾雾”的镜头,这通常是采用“背景拍摄法”:让演员站在平台上,做着飞行的动作,在他的背后展现出蓝天和急速飘动的白云,同时加上烟雾效果;摄影师把人物动作和飘动的白云及下面的烟雾等一起摄入镜头.放映时,观众就感觉到演员在“腾云驾雾”.这时,观众所选的参考系是( )
| A. | 演员 | B. | 平台 | C. | 飘动的白云 | D. | 镜头 |
15.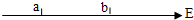 如图所示为真空中一个静止的负点电荷形成电场中的一条电场线,用Ea、Eb分别表示a、b两点的电场强度大小,用φa、φb分别表示a、b两点的电势高低则( )
如图所示为真空中一个静止的负点电荷形成电场中的一条电场线,用Ea、Eb分别表示a、b两点的电场强度大小,用φa、φb分别表示a、b两点的电势高低则( )
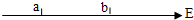 如图所示为真空中一个静止的负点电荷形成电场中的一条电场线,用Ea、Eb分别表示a、b两点的电场强度大小,用φa、φb分别表示a、b两点的电势高低则( )
如图所示为真空中一个静止的负点电荷形成电场中的一条电场线,用Ea、Eb分别表示a、b两点的电场强度大小,用φa、φb分别表示a、b两点的电势高低则( )| A. | Ea>Eb | B. | Ea<Eb | C. | φa>φb | D. | φa<φb |
12.宇宙中两颗星球可以组成双星,它们只在相互间的万有引力作用下,绕球心连线的某点做周期相同的匀速圆周运动.根据宇宙大爆炸理论,双星间的距离在不断缓慢增加,设双星仍做匀速圆周运动.则下列说法正确的是( )
| A. | 双星相互间的万有引力减小 | B. | 双星做圆周运动的半径减小 | ||
| C. | 双星做圆周运动的周期减小 | D. | 双星做圆周运动的线速度减小 |
19.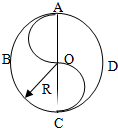 如图所示,是一个半径为R的中国古代八卦图,中央S部分是两个半圆,练功人从A点出发沿相关路线(有半个圆、中间两个半圆和中间直线三条路线)进行(不能重复),在最后到达C点.求此人在运动的最大路程和位移大小分别为( )
如图所示,是一个半径为R的中国古代八卦图,中央S部分是两个半圆,练功人从A点出发沿相关路线(有半个圆、中间两个半圆和中间直线三条路线)进行(不能重复),在最后到达C点.求此人在运动的最大路程和位移大小分别为( )
 如图所示,是一个半径为R的中国古代八卦图,中央S部分是两个半圆,练功人从A点出发沿相关路线(有半个圆、中间两个半圆和中间直线三条路线)进行(不能重复),在最后到达C点.求此人在运动的最大路程和位移大小分别为( )
如图所示,是一个半径为R的中国古代八卦图,中央S部分是两个半圆,练功人从A点出发沿相关路线(有半个圆、中间两个半圆和中间直线三条路线)进行(不能重复),在最后到达C点.求此人在运动的最大路程和位移大小分别为( )| A. | (3π+2)R,2R | B. | πR,2R | C. | (3π+2)R,4R | D. | (3π+2)R,0 |
16.下列说法中不正确的一项是( )
| A. | 在国际单位制中,力的单位“N”属于导出单位 | |
| B. | 使质量为1kg的物体产生1m/s2的加速度的力的大小就是1N | |
| C. | 静电力常量k是由英国科学家卡文迪许首次通过扭秤实验测出 | |
| D. | 点电荷是物理学中一种理想化模型 |
13.一位同学沿着周长为400m的学校运动场跑了1圈,他的路程和位移大小分别是( )
| A. | 400,400 | B. | 0,400 | C. | 400,0 | D. | 0,0 |
 电梯上升运动的v--t图如图3所示,从图象可知:
电梯上升运动的v--t图如图3所示,从图象可知: