题目内容
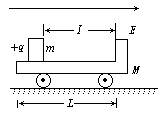
一个质量为M的绝缘小车,静止在光滑水平面上,在小车的光滑板面上放一个质量为m、带电荷量为+q的带电小物块(可视为质点),小车质量与物块质量之比M∶m=7∶1,物块距小车右端挡板距离为l,小车车长为L,且L=1.5l,如图所示,现沿平行车身方向加一电场强度为E的水平向右的匀强电场,带电小物块由静止开始向右运动,之后与小车右端挡板相碰,若碰后小车速度大小为碰撞前小物快速度大小的1/4,并设小物块滑动过程及其与小车相碰的过程中,小物块带电荷量不变.通过分析与计算说明,碰撞后滑块能否滑出小车的车身?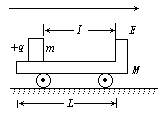
答案:
解析:
提示:
解析:
| 解:滑块从静止到和车右端相撞过程,由动能定理得:
qEl= 第一次相碰后小车速度v2=v0/4, 设滑块这时速度为v1 由mv0=mv1+ 设滑块不滑出小车,第一次碰后到两者具有相同速度v2时,滑块发生的位移为S1,小车发生的位移为S2,历时为t. 滑块:作加速度相同的向左匀减速和向右匀加速(看作同一匀变速), a= 又由v2=v1+at 得t= 小车:作向右匀速运动:S2=v2t=l/2. ∵ S2-S1=l<L=1.5l,∴ 滑块不会滑出小车.
|
提示:

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
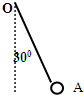 如图,在场强为E的匀强电场中有一个质量为m的带正电小球A悬挂在绝缘细线上,当小球静止时,细线与竖直方向成30°角,己知此电场方向恰使小球受到的电场力最小,则小球所带的电量应为( )
如图,在场强为E的匀强电场中有一个质量为m的带正电小球A悬挂在绝缘细线上,当小球静止时,细线与竖直方向成30°角,己知此电场方向恰使小球受到的电场力最小,则小球所带的电量应为( ) 如图所示,在光滑水平面上有一辆长为L、质量为m的绝缘木板小车正以向右的初速度v1=
如图所示,在光滑水平面上有一辆长为L、质量为m的绝缘木板小车正以向右的初速度v1=