题目内容
15.如图,a、b、c是在地球大气层外圆形轨道上运行的三颗人造地球卫星,下列说法中正确的是( )
| A. | b、c的线速度大小相等,且小于a的线速度 | |
| B. | b、c的向心加速度大小相等,且大于a的向心加速度 | |
| C. | c加速(速率增大)可追上同一轨道上的b | |
| D. | b、c周期相等,且大于a的周期 |
分析 卫星绕地球做圆周运动,万有引力提供向心力,应用牛顿第二定律与向心力公式求出加速度、周期、线速度,然后分析答题.
解答 解:由图示可知:ra<rb=rc,卫星绕地球做圆周运动,万有引力提供向心力;
A、由牛顿第二定律得:G$\frac{Mm}{{r}^{2}}$=m$\frac{{v}^{2}}{r}$,解得:v=$\sqrt{\frac{GM}{r}}$,由ra<rb=rc可知,b、c的线速度大小相等且小于a的线速度大小,故A正确;
B、由牛顿第二定律得:G$\frac{Mm}{{r}^{2}}$=ma,解得:a=$\frac{GM}{{r}^{2}}$,由ra<rb=rc可知,b、c的向心加速度大小相等且小于a的向心加速度,故B错误;
C、c加速,c的速度增大,做圆周运动需要的向心力增大,需要的向心力大于卫星与地球间的万有引力,c要做离心运动,c不能追上b,故C错误;
C、由牛顿第二定律得:G$\frac{Mm}{{r}^{2}}$=m$(\frac{2π}{T})^{2}$r,解得:T=2π$\sqrt{\frac{{r}^{3}}{GM}}$,由ra<rb=rc可知,b、c的向心周期相等且大于a的周期,故D正确;
故选:AD.
点评 本题考查了万有引力定律的应用,考查了比较向心加速度、线速度、周期大小关系,由图示求出卫星间的轨道半径关系是正确解题的关键,应用万有引力公式与牛顿第二定律可以解题.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
5. 一质量为m的小球以初动能EK0冲上倾角为θ的粗糙斜面,图中两条图线分别表示小球在上升过程中动能、重力势能中的某一个与其上升高度之间的关系(以斜面底端为零势能面,h0表示上升的最大高度,图中坐标数据中的k为常数且满足0<k<1),则由图可知,下列结论正确的是( )
一质量为m的小球以初动能EK0冲上倾角为θ的粗糙斜面,图中两条图线分别表示小球在上升过程中动能、重力势能中的某一个与其上升高度之间的关系(以斜面底端为零势能面,h0表示上升的最大高度,图中坐标数据中的k为常数且满足0<k<1),则由图可知,下列结论正确的是( )
 一质量为m的小球以初动能EK0冲上倾角为θ的粗糙斜面,图中两条图线分别表示小球在上升过程中动能、重力势能中的某一个与其上升高度之间的关系(以斜面底端为零势能面,h0表示上升的最大高度,图中坐标数据中的k为常数且满足0<k<1),则由图可知,下列结论正确的是( )
一质量为m的小球以初动能EK0冲上倾角为θ的粗糙斜面,图中两条图线分别表示小球在上升过程中动能、重力势能中的某一个与其上升高度之间的关系(以斜面底端为零势能面,h0表示上升的最大高度,图中坐标数据中的k为常数且满足0<k<1),则由图可知,下列结论正确的是( )| A. | 上升过程中摩擦力大小f=k mgcosθ | |
| B. | 上升过程中摩擦力大小f=k mgsinθ | |
| C. | 上升高度h=$\frac{k+1}{k+2}{h_0}$时,小球重力势能和动能相等 | |
| D. | 上升高度h=$\frac{k+1}{k+2}{h_0}$sinθ时,小球重力势能和动能相等 |
6.如图,电源电动势E=8V,内阻不为零,灯泡A标有“10V,10W“字样,B标有“8V,20W”字样,滑动变阻器的总电阻为6Ω,当滑动触头P由a端向b端滑动的过程中(不考虑电灯电阻的变化)( )

| A. | 电流表的示数一直增大,电压表的示数一直减小 | |
| B. | 电流表的示数一直增大,电压表的示数电压表的示数一直减小 | |
| C. | 电流表的示数先增大后减小,电压表的示数先减小后增大 | |
| D. | 电流表的示数先减小后增大,电压表的示数先增大后减小 |
 如图所示为某同学在“验证机械能守恒定律”实验中得到的一条纸带,图中O点为打点计时器打下的第一点,可以看做重物运动的起点,从后面某点起选取连续打下的三个点A、B、C,已知相邻两点间的时间间隔为0.02s,假设重物的质量为1.00kg,则从起点O到打下B点的过程中,重物动能的增加量△EK=1.84,J重力势能的减少最△EP=1.88J,由此可得出的实验结论是:在误差允许的范围内物体下落过程的机械能守恒(选填“守恒”、“不守恒’或“不确定”).(保留三位有效数字,取重力加速度g=9.80m/s2)
如图所示为某同学在“验证机械能守恒定律”实验中得到的一条纸带,图中O点为打点计时器打下的第一点,可以看做重物运动的起点,从后面某点起选取连续打下的三个点A、B、C,已知相邻两点间的时间间隔为0.02s,假设重物的质量为1.00kg,则从起点O到打下B点的过程中,重物动能的增加量△EK=1.84,J重力势能的减少最△EP=1.88J,由此可得出的实验结论是:在误差允许的范围内物体下落过程的机械能守恒(选填“守恒”、“不守恒’或“不确定”).(保留三位有效数字,取重力加速度g=9.80m/s2)
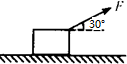 如图,物体在光滑水平面上受到与水平方向成30°角的力F=100N作用,已知物体的重力G=100N,求物体所受支持力的大小与合力的大小.
如图,物体在光滑水平面上受到与水平方向成30°角的力F=100N作用,已知物体的重力G=100N,求物体所受支持力的大小与合力的大小. 交流发电机的发电原理是矩形线圈在匀强磁场中绕垂直于磁场的轴OO′匀速转动.一小型发电机的线圈共220匝,线圈面积S=0.05m2,线圈转动的频率为50Hz,线圈内阻不计,磁场的磁感应强度B=$\frac{\sqrt{2}}{π}$ T.为用此发电机所发出交变电流带动两个标有“220V,11kW”的电机正常工作,需在发电机的输出端a、b与电机之间接一个理想变压器,电路如图所示,求:
交流发电机的发电原理是矩形线圈在匀强磁场中绕垂直于磁场的轴OO′匀速转动.一小型发电机的线圈共220匝,线圈面积S=0.05m2,线圈转动的频率为50Hz,线圈内阻不计,磁场的磁感应强度B=$\frac{\sqrt{2}}{π}$ T.为用此发电机所发出交变电流带动两个标有“220V,11kW”的电机正常工作,需在发电机的输出端a、b与电机之间接一个理想变压器,电路如图所示,求: